
分析 (1)先求出曲线C的普通方程,再由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,能求出曲线C的极坐标方程.
(2)设曲线C上存在点P(3+cosα,4+sinα),使得∠APB=90°,从而$\overrightarrow{AP}•\overrightarrow{BP}$=(a+3+cosα,4+sinα)•(-a+3+cosα,4+sinα)=0,由此利用三角函数性质能求出实数a的取值范围.
解答 解:(1)∵曲线C的参数方程为$\left\{\begin{array}{l}{x=3+cosα}\\{y=4+sinα}\end{array}\right.$(α为参数),
∴曲线C的普通方程为(x-3)2+(y-4)2=1,
即x2+y2-6x-8y+24=0,
由ρ2=x2+y2,x=ρcosθ,y=ρsinθ,
得曲线C的极坐标方程为ρ2-6ρcosθ-8ρsinθ+24=0.
(2)设曲线C上存在点P(3+cosα,4+sinα),使得∠APB=90°,
∵A(-a,0),B(a,0)(a>0),
∴$\overrightarrow{AP}•\overrightarrow{BP}$=(a+3+cosα,4+sinα)•(-a+3+cosα,4+sinα)=0,
∴a2=8sinα+6cosα+26=10sin(α+θ)+26≤36,
又∵a>0,
∴实数a的取值范围是(0,6].
点评 本题考查曲线的极坐标方程的求法,考查实数的取值范围的求法,是基础题,解题时要注意直角坐标和极坐标互化公式的合理运用.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2015-2016学年四川成都石室中学高二文下期中数学试卷(解析版) 题型:选择题
已知动点 到点
到点 和到直线
和到直线 的距离相等,则动点
的距离相等,则动点 的轨迹是( )
的轨迹是( )
A.抛物线 B.双曲线左支 C.一条直线 D.圆
查看答案和解析>>
科目:高中数学 来源:2015-2016学年四川成都石室中学高二理下期中数学试卷(解析版) 题型:选择题
如图,网格纸上正方形小格的边长为 ,图中粗线画出的是某几何体的三视图,则几何体的体积为( )
,图中粗线画出的是某几何体的三视图,则几何体的体积为( )

A.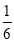 B.
B.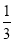 C.
C.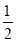 D.
D.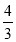
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com