
分析 与$\frac{{y}^{2}}{4}$-x2=1有相同的渐近线的方程可设为$\frac{{y}^{2}}{4}$-x2=λ≠0,再把点P的坐标代入即可.
解答 解:依题设所求双曲线方程为$\frac{{y}^{2}}{4}$-x2=λ≠0,
∵双曲线过点P(2,2),
∴1-4=λ,
∴λ=-3
∴所求双曲线方程为$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{12}=1$.
点评 本题考查双曲线方程的求法,正确利用:与$\frac{{y}^{2}}{4}$-x2=1有相同的渐近线的方程可设为$\frac{{y}^{2}}{4}$-x2=λ≠0,是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,1) | C. | (-1,$\frac{1}{5}$) | D. | (-$\frac{1}{5}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$±\sqrt{2}$x | B. | y=±$\frac{\sqrt{7}}{3}$x | C. | y=±$\frac{4}{3}$x | D. | y=±$\sqrt{6}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
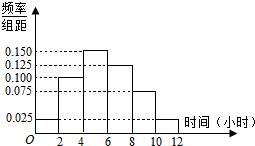 某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).
某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 中位数>平均数>众数 | B. | 众数>中位数>平均数 | ||
| C. | 众数>平均数>中位数 | D. | 平均数>众数>中位数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com