
| y-1 | x+1 |
| y-1 |
| x+1 |


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
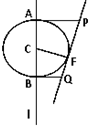 (2007•湛江二模)如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l相交于A、B两点,过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q,则必在以F为焦点,l为准线的同一条抛物线上.
(2007•湛江二模)如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l相交于A、B两点,过A、B分别作l的垂线与圆C过F的切线相交于点P和点Q,则必在以F为焦点,l为准线的同一条抛物线上.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
如图,F是定直线l外的一个定点,C是l上的动点,有下列结论:若以C为圆心,CF为半径的圆与l交于A、B两点,过A、B分别作l的垂线与圆
C过F的切线交于点P和点Q,则P、Q必在以F为焦点,l为准线的同一条抛物线上.
(Ⅰ)建立适当的坐标系,求出该抛物线的方程;
(Ⅱ)对以上结论的反向思考可以得到另一个命题:
“若过抛物线焦点F的直线与抛物线交于P、Q两点,
则以PQ为直径的圆一定与抛物线的准线l相切”请
问:此命题是否正确?试证明你的判断;
(Ⅲ)请选择椭圆或双曲线之一类比(Ⅱ)写出相应的命题并
证明其真假.(只选择一种曲线解答即可,若两种都选,则以第一选择为评分依据)
查看答案和解析>>
科目:高中数学 来源:2013届贵州省高一下学期期末考试数学 题型:选择题
下列结论正确的是( )
(A)若直线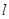 平行于面
平行于面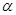 内的无数条直线,则
内的无数条直线,则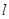 ∥
∥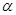
(B)过直线外一点有且只有一个平面和该直线平行
(C)若直线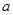 ∥直线
∥直线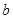 ,直线
,直线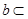 平面
平面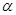 ,则
,则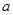 平行于
平行于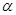 内的无数条直线
内的无数条直线
(D)若两条直线都和第三条直线垂直,则这两条直线平行
查看答案和解析>>
科目:高中数学 来源:2009-2010学年福建省三明市五校联考高二(上)期中数学试卷(必修2)(解析版) 题型:填空题
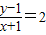 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com