
(本小题满分12分)已知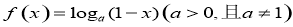
(1)求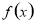 的定义域;
的定义域;
(2)求使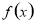 >0成立的x的取值范围.
>0成立的x的取值范围.
(1)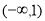 (2)当
(2)当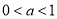 时,
时, 的取值范围是
的取值范围是 ;当
;当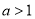 时,
时, 的取值范围是
的取值范围是
【解析】
试题分析:本体题第一步求函数的定义域,掌握对数的真数大于零即可;第二步解不等式,要注意底数
的范围 且
且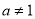 ,由于当
,由于当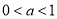 时,对数函数
时,对数函数 是
是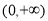 上的增函数;而当
上的增函数;而当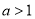 时,对数函数
时,对数函数 是
是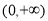 上的减函数;因此在解不等式时,就要分类讨论,利用同底法或用指对互化均可,但应注意不等号的方向及对数真数大于零。
上的减函数;因此在解不等式时,就要分类讨论,利用同底法或用指对互化均可,但应注意不等号的方向及对数真数大于零。
试题解析:(1)函数解析式为对数函数型,要使 有意义,只要真数大于零即可,由
有意义,只要真数大于零即可,由 则
则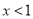 ,
,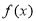 的定义域为
的定义域为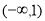 ;
;
由于当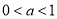 时,对数函数
时,对数函数 是
是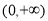 上的增函数;而当
上的增函数;而当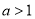 时,对数函数
时,对数函数 是
是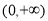 上的减函数;所以解不等式
上的减函数;所以解不等式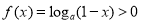 需要对
需要对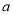 进行讨论,还要注意不等号的方向。
进行讨论,还要注意不等号的方向。
?当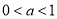 时,
时,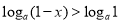 ,
,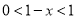 ,解得
,解得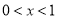
?当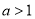 时,
时,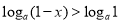 ,
, ,解得
,解得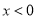
综上所述:当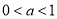 时,
时, 的取值范围是
的取值范围是 ;当
;当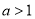 时,
时, 的取值范围是
的取值范围是
考点:1.求函数的定义域2.对数函数的图象与性质;3.解对数不等式


科目:高中数学 来源:2015届豫晋冀高三第二次调研考试理科数学试卷(解析版) 题型:选择题
已知双曲线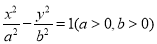 的一条渐近线与圆
的一条渐近线与圆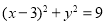 相变于A.B两点,若
相变于A.B两点,若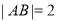 ,则该双曲线的离心率为( )
,则该双曲线的离心率为( )
A.8 B.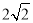 C 3 D.4
C 3 D.4
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:填空题
某运动队有男女运动员49人,其中男运动员有28人,按男女比例用分层抽样的方法,从全体运动员中抽出一个容量为14的样本,那么应抽取女运动员人数是 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖北省襄阳市高三上学期11月质检文科数学试卷(解析版) 题型:选择题
已知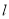 ,
, 是三条不同直线,
是三条不同直线,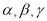 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( )
A.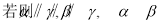
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省赣州市十二县高二上学期期中联考文科数学试卷(解析版) 题型:解答题
(本题满分12分)已知集合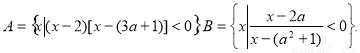
(1)当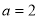 时,求
时,求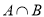 ;
;
(2)当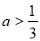 时,求使
时,求使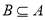 的实数
的实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com