练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知数列{an}是等差数列，其前n项和为Sn，若S2017=4034，则a3+a1009+a2015=（　　）
    A．2B．4C．6D．8

    分析 由${S}_{2017}=\frac{2017}{2}（{a}_{1}+{a}_{2017}）$=2017a1009=4034，得a1009=2，由等差数列的通项公式得a3+a1009+a2015=3a1009，由此能求出结果．

    解答 解：∵数列{an}是等差数列，其前n项和为Sn，S2017=4034，
    ∴${S}_{2017}=\frac{2017}{2}（{a}_{1}+{a}_{2017}）$=2017a1009=4034，
    ∴a1009=2，
    ∴a3+a1009+a2015=3a1009=6．
    故选：C．

    点评 本题考查等差数列的三项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    11．现有4种不同的颜色为“严勤活实”四个字涂颜色，要求相邻的两个字涂色不同，则不同的涂色种数为（　　）
    A．27B．54C．108D．144

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

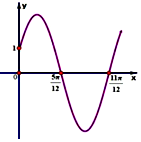    12．已知函数f（x）=Asin（ωx+φ） （x∈R，ω＞0，0＜φ＜$\frac{π}{2}$） 的部分图象如图所示．
    （1）求函数f（x）的解析式．
    （2）求函数g（x）=f（x-$\frac{π}{12}$）-f（x+$\frac{π}{12}$）的单调递增区间．
    （3）若方程g（x）=m在（$\frac{π}{4}$，π]上有两个不相等的实数根，求m的取值范围，并写出所有根之和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知函数$f（x）=\frac{2}{4^x}-x$，设a=0，b=log0.42，c=log43，则有（　　）
    A．f（a）＜f（c）＜f（b）B．f（c）＜f（b）＜f（a）C．f（a）＜f（b）＜f（c）D．f（b）＜f（c）＜f（a）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=Asin（wx+φ）（A＞0，w＞0，0＜φ＜$\frac{π}{2}$）的最小正周期为π，且图象上一个最低点为$M（\frac{2π}{3}，-2）$
    （1）求f（x）的解析式
    （2）当$x∈[{0，\frac{π}{2}}]$，求f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．${（{\frac{2+2i}{1-i}}）^3}$=（　　）
    A．8B．-8C．8iD．-8i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．复数$\frac{i}{1+i}$（i是虚数单位）的实部是（　　）
    A．2B．-2C．-$\frac{1}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知α∈[0，2π），直线l1：xcosα-y-1=0，l2：x+ysinα+1=0相互垂直，则α的值为$\frac{π}{4}$或$\frac{5π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

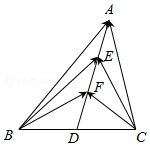    11．如图，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，$\overrightarrow{BA}•\overrightarrow{CA}=8$，$\overrightarrow{BF}•\overrightarrow{CF}=-2$则$\overrightarrow{BE}•\overrightarrow{CE}$的值是$\frac{7}{4}$．

    查看答案和解析>>

    同步练习册答案