
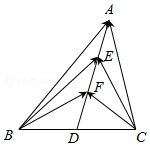
 ��ͼ���ڡ�ABC�У�D��BC���е㣬E��F��AD�ϵ��������ȷֵ㣬$\overrightarrow{BA}•\overrightarrow{CA}=8$��$\overrightarrow{BF}•\overrightarrow{CF}=-2$��$\overrightarrow{BE}•\overrightarrow{CE}$��ֵ��$\frac{7}{4}$��
��ͼ���ڡ�ABC�У�D��BC���е㣬E��F��AD�ϵ��������ȷֵ㣬$\overrightarrow{BA}•\overrightarrow{CA}=8$��$\overrightarrow{BF}•\overrightarrow{CF}=-2$��$\overrightarrow{BE}•\overrightarrow{CE}$��ֵ��$\frac{7}{4}$�� ���� ���������ļӼ��ļ�����������������������������
��� �⣺D��BC���е㣬E��F��AD�ϵ��������ȷֵ㣬
��$\overrightarrow{BF}$=$\overrightarrow{BD}$+$\overrightarrow{DF}$��$\overrightarrow{CF}$=-$\overrightarrow{BD}$+$\overrightarrow{DF}$��$\overrightarrow{BA}$=$\overrightarrow{BD}$+3$\overrightarrow{DF}$��$\overrightarrow{CA}$=-$\overrightarrow{BD}$+3$\overrightarrow{DF}$��
��$\overrightarrow{BF}•\overrightarrow{CF}$=${\overrightarrow{DF}}^{2}$-${\overrightarrow{BD}}^{2}$=-2��
$\overrightarrow{BA}•\overrightarrow{CA}$=9${\overrightarrow{DF}}^{2}$-${\overrightarrow{BD}}^{2}$=8��
��${\overrightarrow{DF}}^{2}$=$\frac{5}{4}$��${\overrightarrow{BD}}^{2}$=$\frac{13}{4}$��
��$\overrightarrow{BE}$=$\overrightarrow{BD}$+2$\overrightarrow{DF}$��$\overrightarrow{CE}$=-$\overrightarrow{BD}$+2$\overrightarrow{DF}$��
��$\overrightarrow{BE}•\overrightarrow{CE}$=4${\overrightarrow{DF}}^{2}$-${\overrightarrow{BD}}^{2}$=4��$\frac{5}{4}$-$\frac{13}{4}$=$\frac{7}{4}$
�ʴ�Ϊ��$\frac{7}{4}$
���� ���⿼���֪ʶ��ƽ�����������������㣬ƽ���������������㣬�Ѷ��е���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 6 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 2 | 4 | 5 | 6 | 8 |
| y | 40 | 60 | 50 | 70 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������O-ABCD�У�����ABCD�DZ߳�Ϊ1�����Σ���ABC=$\frac{��}{4}$��OA�͵���ABCD��OA=2��MΪOA���е㣬NΪBC���е㣮
��ͼ��������O-ABCD�У�����ABCD�DZ߳�Ϊ1�����Σ���ABC=$\frac{��}{4}$��OA�͵���ABCD��OA=2��MΪOA���е㣬NΪBC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 60�� | B�� | 120�� | C�� | 135�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B�� | $\frac{x^2}{20}-\frac{y^2}{100}=1$ | C�� | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D�� | $\frac{x^2}{25}-\frac{y^2}{100}=1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾΪ�ⳤΪ1��������ı���չ��ͼ����ԭ�������У����������ĸ����ۣ�
��ͼ��ʾΪ�ⳤΪ1��������ı���չ��ͼ����ԭ�������У����������ĸ����ۣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com