
设在一个盒子中,放有标号分别为1,2,3的三张卡片,现从这个盒子中,有放回地先后抽得两张卡片,标号分别记为 ,设随机变量
,设随机变量 .
.
(1)写出 的可能取值,并求随机变量
的可能取值,并求随机变量 的最大值;
的最大值;
(2)求事件“ 取得最大值”的概率;
取得最大值”的概率;
(3)求 的分布列和数学期望与方差.
的分布列和数学期望与方差.
(1)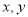 的可能取值为1,2,3;
的可能取值为1,2,3;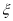 的最大值3;(2)
的最大值3;(2)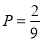 ;(3)
;(3)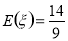 ,
,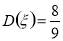
【解析】
试题分析:(1)求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(2)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(3)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
试题解析:【解析】
(1)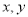 的可能取值都为1,2,3.
的可能取值都为1,2,3.
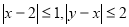 ,∴
,∴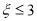 ,
,
∴当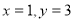 或
或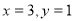 时,
时,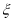 取最大值
取最大值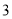 . 3分
. 3分
(2)有放回地先后抽得两张卡片的所有情况的种数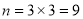 ,
,
∴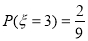 4分
4分
(3)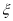 的所有取值为0,1,2,3,
的所有取值为0,1,2,3,
当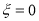 时,只有
时,只有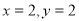 这1种情况,∴
这1种情况,∴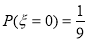 ;
;
当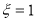 时,只有
时,只有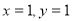 或
或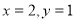 或
或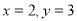 或
或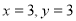 ,
,
共4种情况,∴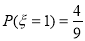 ;
;
当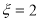 时,只有
时,只有 这2种情况,∴
这2种情况,∴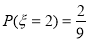 ;
;
当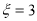 时,
时,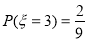 ; 7分
; 7分
∴ 随机变量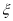 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴ 数学期望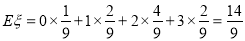
方差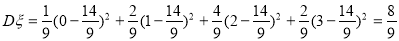 9分
9分
考点:求离散型随机变量的分布列、数学期望、方差.


科目:高中数学 来源:2015届山东省文登市高二下学期期末理科数学试卷(解析版) 题型:选择题
一个袋子里装有编号为 的
的 个相同大小的小球,其中
个相同大小的小球,其中 到
到 号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是
号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是
A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com