
已知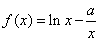
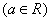 .
.
(Ⅰ)判断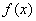 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若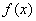 在
在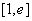 上的最小值为
上的最小值为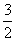 ,求
,求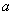 的值;
的值;
(III)若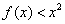 在
在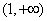 上恒成立,试求
上恒成立,试求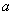 的取值范围.
的取值范围.
解:(Ⅰ)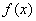 的定义域为
的定义域为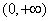
 …………………………1分
…………………………1分
当 时,
时,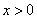
∴ 因此
因此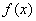 在定义域
在定义域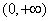 上为单调递增函数.……………………2分
上为单调递增函数.……………………2分
当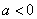 时,则
时,则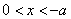 ,
,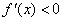 ;
;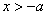 ,
, ;
;
此时,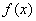 在
在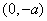 上为单调递增函数,在
上为单调递增函数,在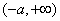 上为单调递增函数.…………4分
上为单调递增函数.…………4分
(Ⅱ)(1)令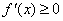 在
在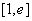 上恒成立,即
上恒成立,即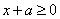
∴ .
.
令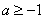 ,此时
,此时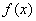 在
在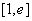 上为增函数.
上为增函数.
∴ ,
,
得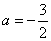 (舍去).…………………………6分
(舍去).…………………………6分
(2)令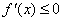 在
在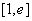 上恒成立,即
上恒成立,即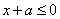
∴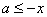 .
.
令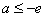 ,此时
,此时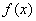 在
在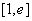 上为减函数.
上为减函数.
∴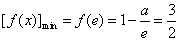 ,
,
得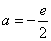 (舍去).…………………………8分
(舍去).…………………………8分
(3)当时,令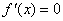 ,得
,得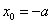 .
.
当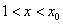 时,
时,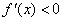 ,∴
,∴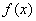 在
在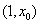 上为减函数.
上为减函数.
当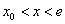 时,
时, ,∴
,∴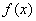 在
在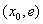 上为增函数.
上为增函数.
∴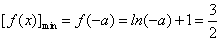
得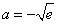 .
.
综上可知,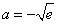 .…………………………10分
.…………………………10分
(III)由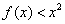 ,得
,得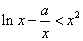 ,
,
∵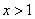 ,∴有
,∴有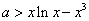 ,
,
令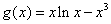 ,则
,则 .…………………………12分
.…………………………12分
令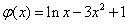 ,则
,则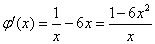 ,
,
∵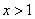 ,∴
,∴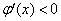 ,∴
,∴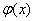 在
在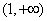 上单调递减,
上单调递减,
∴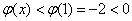 ,
,
因此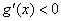 ,故
,故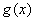 在
在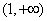 上单调递减,…………………………14分
上单调递减,…………………………14分
则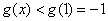 ,
,
∴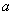 的取值范围是
的取值范围是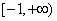 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
为考察高中生的性别与是否喜欢数学课程之间的关系,在某城市的某校高中生中随机抽取100名学生,其中男生喜欢数学课程的20人,不喜欢数学课程的30人;女生喜欢数学课程的10人,不喜欢数学课程的40人。
(Ⅰ)根据以上数据作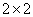 列联表;(答案填写在答题纸上)
列联表;(答案填写在答题纸上)
| 喜欢数学课程 | 不喜欢数学课程 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
(Ⅱ)根据以上数据,能否有95%的把握认为“高中生的性别与是否喜欢数学课程有关”?
|
| 0.050 | 0.010 | 0.001 |
|
| 3.841 | 6.635 | 10.828 |
附: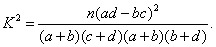
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com