
【题目】直线x+y=1与双曲线 ![]() =1 (a>0,b>0)交于M、N两点,若以M、N两点为直径的圆经过坐标原点O.
=1 (a>0,b>0)交于M、N两点,若以M、N两点为直径的圆经过坐标原点O.
(1)求 ![]() 的值;
的值;
(2)若0<a≤ ![]() ,求双曲线离心率e的取值范围.
,求双曲线离心率e的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①已知M={(x,y)| ![]() =3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
=3},N={(x,y)|ax+2y+a=0}且M∩N=,则a=﹣6;
②已知点A(x1 , y1),B(x2 , y2),则以AB为直径的圆的方程是(x﹣x1)(x﹣x2)+(y﹣y1)(y﹣y2)=0;
③ ![]() =1(a≠b)表示焦点在x轴上的椭圆;
=1(a≠b)表示焦点在x轴上的椭圆;
④已知抛物线y2=2px(p>0)的焦点弦AB的两端点坐标分别为A(x1 , y2),B(x2 , y2),则 ![]() =﹣4
=﹣4
其中的真命题是 . (把你认为是真命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P是曲线C: ![]() ﹣y2=1上的任意一点,直线l:x=2与双曲线C的渐近线交于A,B两点,若
﹣y2=1上的任意一点,直线l:x=2与双曲线C的渐近线交于A,B两点,若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,(λ,μ∈R,O为坐标原点),则下列不等式恒成立的是( )
,(λ,μ∈R,O为坐标原点),则下列不等式恒成立的是( )
A.λ2+μ2≥ ![]()
B.λ2+μ2≥2
C.λ2+μ2≤ ![]()
D.λ2+μ2≤2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了估计某校的一次数学考试情况,现从该校参加考试的600名学生中随机抽出60名学生,其成绩(百分制)均在[40,100)上,将这些成绩分成六段[40,50),[50,60)…[90,100),后得到如图所示部分频率分布直方图. 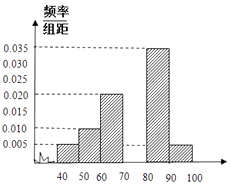
(1)求抽出的60名学生中分数在[70,80)内的人数;
(2)若规定成绩不小于85分为优秀,则根据频率分布直方图,估计该校优秀人数.
(3)根据频率分布直方图算出样本数据的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记函数f(x)= ![]() 的定义域为集合A,则函数g(x)=
的定义域为集合A,则函数g(x)= ![]() 的定义域为集合B,
的定义域为集合B,
(1)求A∩B和A∪B
(2)若C={x|p﹣2<x<2p+1},且CA,求实数p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点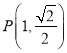 ,且
,且![]() 的离心率为
的离心率为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的顶点
的顶点![]() 作两条互相垂直的直线与椭圆分别相交于
作两条互相垂直的直线与椭圆分别相交于![]() 两点.若
两点.若![]() 的角平分线方程为
的角平分线方程为![]() ,求
,求![]() 的面积及直线
的面积及直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各组函数表示相同函数的是( )
A.f(x)= ![]() ,g(x)=(
,g(x)=( ![]() )2
)2
B.f(x)=1,g(x)=x2
C.f(x)= ![]() ,g(t)=|t|
,g(t)=|t|
D.f(x)=x+1,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017江西上饶联考】某种药种植基地有两处种植区的药材需在下周一、周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘,由于下雨会影响药材的收益,若基地收益如下表所示:已知下周一和下周二无雨的概率相同且为![]() ,两天是否下雨互不影响,若两天都下雨的概率为
,两天是否下雨互不影响,若两天都下雨的概率为![]()

(1)求![]() 及基地的预期收益;
及基地的预期收益;
(2)若该基地额外聘请工人,可在周一当天完成全部采摘任务,若周一无雨时收益为![]() 万元,有雨时收益为
万元,有雨时收益为![]() 万元,且额外聘请工人的成本为
万元,且额外聘请工人的成本为![]() 元,问该基地是否应该额外聘请工人,请说明理由.
元,问该基地是否应该额外聘请工人,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com