
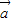 =(1,1),向量
=(1,1),向量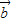 与
与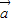 的夹角为
的夹角为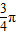 ,且
,且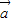 •
•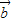 =-1.
=-1.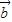 ;
;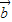 与
与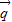 =(1,0)的夹角为
=(1,0)的夹角为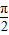 ,而向量
,而向量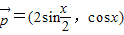 ,试求f(x)=
,试求f(x)=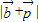 ;
;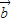 =(x,y),利用向量
=(x,y),利用向量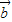 与
与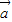 的夹角为
的夹角为 ,且
,且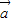 •
•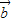 =-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.
=-1.得到 x+y=-1与 x2+y2=1,解方程求出x,y即可.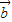 与
与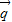 =(1,0)的夹角为
=(1,0)的夹角为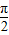 ,判断
,判断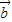 =(0,-1),表示
=(0,-1),表示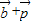 ,然后利用向量的模的求法求出
,然后利用向量的模的求法求出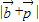 .
.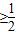 ,通过函数的单调性求出f(x)的值域即可.
,通过函数的单调性求出f(x)的值域即可.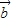 =(x,y)
=(x,y)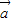 •
•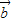 =-1,
=-1,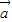 •
•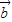 =|a||
=|a||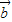 |cosΘ=1×x+1×y=x+y
|cosΘ=1×x+1×y=x+y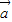 ||
||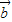 |cos
|cos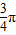 =-
=-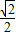 |
|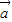 ||
||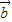 |=-
|=-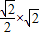 |
|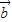 |=-|
|=-|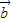 |
|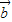 |=1
|=1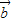 =(0,-1),或
=(0,-1),或 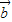 =(-1,0)
=(-1,0)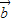 与
与 =(1,0)的夹角为
=(1,0)的夹角为 ,所以
,所以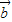 =(0,-1),
=(0,-1), ,
,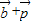 =
= ,
,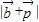 =
=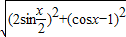 =
=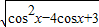
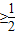 ,
,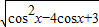 ,1≥cosx
,1≥cosx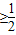 ,
,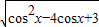 =
=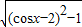 在1≥cosx
在1≥cosx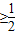 上是减函数,
上是减函数,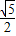 ]
]

科目:高中数学 来源: 题型:
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| n |
| n |
| a |
| b |
| π |
| 3 |
| x |
| 2 |
| a |
| n |
| m |
| n |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| 3 |
| 4 |
| a |
| b |
| b |
| b |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| 2 |
| 3 |
| b |
| p |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| π |
| 2 |
| 1 |
| 5 |
| sin2α-2sin2α |
| 1-tanα |
查看答案和解析>>
科目:高中数学 来源:设计选修数学2-1苏教版 苏教版 题型:013
已知向量a=(1,1,0),b=(-1,0,2)且ka+b与2a-b互相垂直,则k的值是
1
![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分12分)已知向量a=(1,1),b=(1,0),c满足a·c=0且|a|=|c|,b·c>0.
(1)求向量c;(2)若映射f:(x,y)→(x1,y1)=xa+yc,求映射f下(1,2)的原象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com