
已知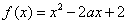 .
.
(Ⅰ) 若不等式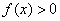 在区间
在区间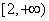 上恒成立,求实数
上恒成立,求实数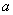 的取值范围;
的取值范围;
(Ⅱ) 解关于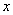 的不等式
的不等式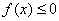 .
.
(1) (2){x|a-
(2){x|a-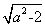 ≤x≤a+
≤x≤a+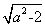 }.
}.
【解析】
试题分析:解: (Ⅰ) 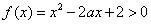 在区间
在区间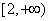 上恒成立,即
上恒成立,即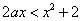 ,
,
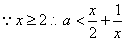 ,
2分
,
2分
令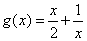 ,
,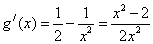 ,
,
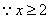 ,
,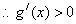 ,
,
所以g(x)在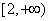 上是增函数,
上是增函数,
所以g(x)的最小值是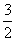 .
.
则实数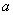 的取值范围是
的取值范围是 .
5分
.
5分
(Ⅱ)∵Δ=4a2-8,
∴当Δ<0,即-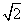 <a<
<a<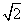 时,
时,
原不等式对应的方程无实根,原不等式的解集为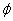 ; 6分
; 6分
当Δ=0,即a=±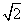 时,原不等式对应的方程有两个相等实根.
时,原不等式对应的方程有两个相等实根.
当a=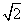 时,原不等式的解集为{x|x=
时,原不等式的解集为{x|x=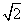 },
},
当a=-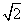 时,原不等式的解集为{x|x=-
时,原不等式的解集为{x|x=-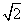 }; 8分
}; 8分
当Δ>0,即a>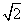 或a<-
或a<-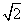 时,原不等式对应的方程有两个不等实根,分别为x1=a-
时,原不等式对应的方程有两个不等实根,分别为x1=a-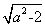 ,x2=a+
,x2=a+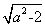 ,且x1<x2,
,且x1<x2,
∴原不等式的解集为{x|a-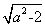 ≤x≤a+
≤x≤a+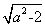 }. 11分
}. 11分
综上,当-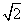 <a<
<a<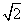 时, 不等式的解集为
时, 不等式的解集为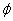 ;当a=
;当a=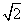 时,不等式的解集为
时,不等式的解集为 };当a=-
};当a=-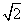 时,不等式的解集为{x|x=-
时,不等式的解集为{x|x=-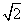 };当a>
};当a>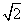 或a<-
或a<-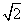 时,不等式的解集为{x|a-
时,不等式的解集为{x|a-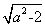 ≤x≤a+
≤x≤a+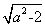 }. 12分
}. 12分
考点:一元二次不等式的解集
点评:主要是考查了二次函数的性质以及二次不等式求解,属于中档题。


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
| 1 | bn |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| 3 |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 2 |
| a |
| 3 |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | bn |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| anan+1 |
| 1 |
| λ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com