
 是一个离散型随机变量,其分布列如下表:求
是一个离散型随机变量,其分布列如下表:求 值,并求
值,并求 .
. |  | 0 | 1 |
 | 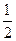 |  |  |
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
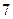 个且形状完全相同,从中任取
个且形状完全相同,从中任取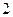 个玩具都是“圆圆”的概率为
个玩具都是“圆圆”的概率为 ,
,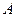 、
、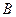 两人不放回从袋中轮流摸取一个玩具,
两人不放回从袋中轮流摸取一个玩具,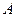 先取,
先取,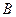 后取,然后
后取,然后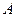 再取,……
再取,…… 直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用
直到两人中有一人取到“圆圆”时即停止游戏.每个玩具在每一次被取出的机会是均等的,用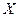 表示游戏终止时取玩具的次数.
表示游戏终止时取玩具的次数.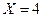 时的概率;
时的概率;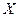 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 对阵队员 | A队队员胜的概率 | A队队员负的概率 |
| A1对B1 | 2 3 | 1 3 |
| A2对B2 | 2 5 | 3 5 |
| A3对B3 | 2 5 | 3 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为
元,若投保人在购买保险的一年度内出险,则可以获得10 000元的赔偿金.假定在一年度内有10 000人购买了这种保险,且各投保人是否出险相互独立.已知保险公司在一年度内至少支付赔偿金10 000元的概率为 。
。 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
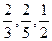 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 2,机器发生故障时全天停止工作
2,机器发生故障时全天停止工作 若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?
若一周5个工作日里均无故障,可获利润10万元;发生一次故障可获利润5万元,只发生两次故障可获利润0万元,发生三次或三次以上故障就要亏损2万元。求一周内期望利润是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
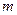 的奖金.假设顾客每次抽奖时获奖与否的概率都是
的奖金.假设顾客每次抽奖时获奖与否的概率都是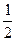 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额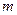 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com