
设f(x)是定义在区间(1,+∞)上的函数,其导函数为f′(x).如果存在实数a和函数h(x),其中h(x)对任意的x∈(1,+∞)都有h(x)>0,使得f′(x)=h(x)(x2-ax+1),则称函数f(x)具有性质P(a).
(1)设函数f(x)=ln x+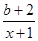 (x>1),其中b为实数.
(x>1),其中b为实数.
①求证:函数f(x)具有性质P(b);
②求函数f(x)的单调区间;
(2)已知函数g(x)具有性质P(2).给定x1,x2∈(1,+∞),x1<x2,设m为实数,α=mx1+(1-m)x2,β=(1-m)x1+mx2,且α>1,β>1,若|g(α)-g(β)|<|g(x1)-g(x2)|,求m的取值范围.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=sinx,g(x)=mx-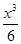 (m为实数).
(m为实数).
(1)求曲线y=f(x)在点P(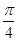 ),f(
),f(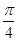 )处的切线方程;
)处的切线方程;
(2)求函数g(x)的单调递减区间;
(3)若m=1,证明:当x>0时,f(x)<g(x)+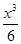 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线 y = x3 + x-2 在点 P0 处的切线  平行直线
平行直线
4x-y-1=0,且点 P0 在第三象限,
求P0的坐标; ⑵若直线 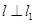 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)(2011•福建)已知a,b为常数,且a≠0,函数f(x)=﹣ax+b+axlnx,f(e)=2(e=2.71828…是自然对数的底数).
(I)求实数b的值;
(II)求函数f(x)的单调区间;
(III)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线y=f(x)(x∈[ ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com