
已知函数f(x)=x3+ax2+bx+c有两个极值点x1,x2,若f(x1)=x1<x2,则关于x的方程3(f(x))2+2af(x)+b=0的不同实根个数为( )
A.3 B.4 C.5 D.6

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:解答题
已知函数f(x)= ax3+(a-2)x+c的图象如图所示.
ax3+(a-2)x+c的图象如图所示.

(1)求函数y=f(x)的解析式;
(2)若g(x)= -2ln x在其定义域内为增函数,求实数k的取值范围.
-2ln x在其定义域内为增函数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:解答题
已知数列{an}的前n项和为Sn,且Sn=2an-2,数列{bn}满足b1=1,且bn+1=bn+2.
(1)求数列{an},{bn}的通项公式;
(2)设cn= an-
an- bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
已知等比数列{an},若存在两项am,an使得am·an=a32,则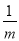 +
+ 的最小值为( )
的最小值为( )
A.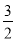 B.
B. C.
C.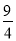 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:解答题
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X,求X的分布列和数学期望;
(2)根据以上数据,我们能否在犯错误的概率不超过0.01的前提下,认为“在20:00-22:00时间段居民的休闲方式与性别有关系”?
参考公式:K2= ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:解答题
(2013·佛山模拟)在平面直角坐标系xOy中,以Ox为始边,角α的终边与单位圆O的交点B在第一象限,已知A(-1,3).
(1)若OA⊥OB,求tan α的值;
(2)若B点横坐标为 ,求S△AOB.
,求S△AOB.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:解答题
已知函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2时,f(x)≤kg(x),求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com