
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() 其图象上任意一点
其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值
的值
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)对函数![]() 进行求导,判断其在
进行求导,判断其在![]() 单调递增,在
单调递增,在![]() 单调递减,从而得到最大值为
单调递减,从而得到最大值为![]() ;
;
(2)求出函数![]() ,
,![]() ,则其导数小于等于
,则其导数小于等于![]() 在
在![]() 恒成立,进而求出
恒成立,进而求出![]() 的取值范围;
的取值范围;
(3)方程![]() 有唯一实数解,设
有唯一实数解,设![]() ,利用导数研究函数
,利用导数研究函数![]() 的图象特征,设
的图象特征,设![]() 为方程的唯一解,得到
为方程的唯一解,得到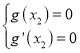 ,把方程组转化成
,把方程组转化成![]() ,再利用导数研究该方程的根,最后根据根的唯一性,得到
,再利用导数研究该方程的根,最后根据根的唯一性,得到![]() 与
与![]() 的关系,再求出正数
的关系,再求出正数![]() 的值.
的值.
(1)依题意,知![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
所以![]() 的极大值为
的极大值为![]() ,此即为最大值.
,此即为最大值.
(2)![]() ,
,![]() ,则有
,则有![]() ,在
,在![]() 上恒成立,所以
上恒成立,所以![]() ,
,![]() .
.
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() .
.
(3)因为方程![]() 有唯一实数解,所以
有唯一实数解,所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,则
,则![]() .
.
令![]() ,
,![]() ,
,
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 取最小值
取最小值![]() .
.
则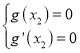 ,即
,即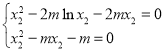 ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]()
设函数![]() ,
,
因为当![]() 时,
时,![]() 是增函数,所以
是增函数,所以![]() 至多有一解,
至多有一解,
又![]() ,所以方程
,所以方程![]() 的解为
的解为![]() ,即
,即![]() ,解得
,解得![]() .
.


科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且2asinA=(2b-c)sinB+(2c-b)sinC..
(1)求角A的大小;
(2)若sinB+sinC=![]() ,试判断△ABC的形状.
,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在工业生产中,对一正三角形薄钢板(厚度不计)进行裁剪可以得到一种梯形钢板零件,现有一边长为3(单位:米)的正三角形钢板(如图),沿平行于边![]() 的直线
的直线![]() 将
将![]() 剪去,得到所需的梯形钢材
剪去,得到所需的梯形钢材![]() ,记这个梯形钢板的周长为
,记这个梯形钢板的周长为![]() (单位:米),面积为
(单位:米),面积为![]() (单位:平方米).
(单位:平方米).
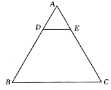
(1)求梯形![]() 的面积
的面积![]() 关于它的周长
关于它的周长![]() 的函数关系式;
的函数关系式;
(2)若在生产中,梯形![]() 的面积与周长之比(即
的面积与周长之比(即![]() )达到最大值时,零件才能符合使用要求,试确定这个梯形的周长
)达到最大值时,零件才能符合使用要求,试确定这个梯形的周长![]() 为多时,该零件才可以在生产中使用?
为多时,该零件才可以在生产中使用?
查看答案和解析>>
科目:高中数学 来源: 题型:
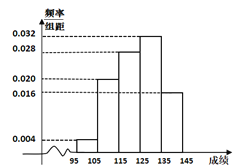
【题目】半期考试后,班长小王统计了50名同学的数学成绩,绘制频率分布直方图如图所示.
![]() 根据频率分布直方图,估计这50名同学的数学平均成绩;
根据频率分布直方图,估计这50名同学的数学平均成绩;
![]() 用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在
用分层抽样的方法从成绩低于115的同学中抽取6名,再在抽取的这6名同学中任选2名,求这两名同学数学成绩均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中燃料费和它的速度的立方成正比.已知速度为每小时10千米时,燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问轮船的速度是多少时,航行1千米所需的费用总和最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司有男性职工64名,一次体检后,将他们的体重(单位:kg)分组为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为
,绘制出频率分布直方图如图,图中从左到右的前3个小组的频率之比为![]() .
.

(1)求这64名男职工中,体重小于60kg的人数;
(2)从体重在![]() kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件
kg范围的男职工中用分层抽样的方法选取6名,再从这6名男职工中随机选取2名,记“至少有一名男职工体重大于65kg”为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
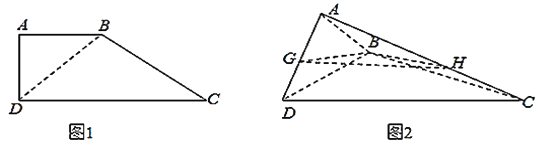
【题目】如图![]() ,直角梯形
,直角梯形![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折起来,使平面
折起来,使平面![]() 平面
平面![]() .如图
.如图![]() ,设
,设![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 的中点为
的中点为![]() .
.
(![]() )求证:
)求证:![]() 平面
平面![]() .
.
(![]() )求平面
)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(![]() )在线段
)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在确定点
,若存在确定点![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com