练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知方程x2+（a-2）x+5-a=0的两个根均大于2，则实数a的取值范围是（-5，-4]．

    分析 设f（x）=x2+（a-2）x+5-a，根据题意利用一元二次方程根的分布与系数的关系，二次函数的性质，求得a的范围．

    解答 解：设f（x）=x2+（a-2）x+5-a，则由方程x2+（a-2）x+5-a=0的两个根均大于2，
    可得$\left\{\begin{array}{l}{△{=（a-2）}^{2}-4（5-a）≥0}\\{-\frac{a-2}{2}＞2}\\{f（2）=a+5＞0}\end{array}\right.$，求得-5＜a≤-4，
    故答案为：（-5，-4]．

    点评 本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    9．如图，在棱长为1的正方体ABCD-A1B1C1D1中，E为AB的中点．求：
    （1）异面直线BD1与CE所成角的余弦值；
    （2）点A到平面A1EC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1的焦点在x轴上，以椭圆右顶点为焦点的抛物线标准方程为y2=16x．
    （1）求椭圆C的离心率
    （2）若动直线l的斜率为$-\frac{{\sqrt{2}}}{2}$，且与椭圆C交于不同的两点M、N，已知点Q$（-\sqrt{2}，0）$，求$\overrightarrow{QM}•\overrightarrow{QN}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．一个五面体的三视图如图，正视图是等腰直角三角形，侧视图是直角三角形，部分边长如图所示，则此五面体的体积为（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．设a=log26，b=log412，c=log618，则（　　）
    A．b＞c＞aB．a＞c＞bC．a＞b＞cD．c＞b＞a

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=m•2x+2•3x，m∈R．
    （1）当m=-9时，求满足f（x+1）＞f（x）的实数x的范围；
    （2）若$f（x）≤{（\frac{9}{2}）^x}$对任意的x∈R恒成立，求实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

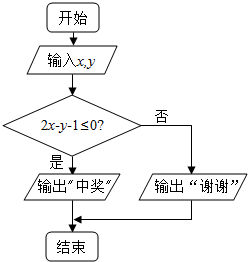    11．某单位抽奖活动的规则是：代表通过操作按键使电脑自动产生两个[0，1]之间的均匀随机数x，y，并按如图所示的程序框图执行．若电脑显示“中奖”，则该代表中奖；若电脑显示“谢谢”，则不中奖，则该代表中奖的概率为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{3}{4}$D．$\frac{2}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=cos（2x-$\frac{π}{3}$）-cos（2x+$\frac{π}{3}$）+2cos2x-1，x∈R．
    （1）求函数f（x）的单调递增区间；
    （2）设向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（2，t）（t≠0），$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为α，若f（α）=1，求实数t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．直线x+a2y+6=0与直线（a-2）x+3ay+2a=0平行，则实数a的值为（　　）
    A．3或-1B．0或-1C．-3或-1D．0或3

    查看答案和解析>>

    同步练习册答案