
【题目】如图,已知长方形ABCD中,AB=2 ![]() ,AD=
,AD= ![]() ,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM.
,M为DC的中点.将△ADM沿AM折起,使得平面ADM⊥平面ABCM. 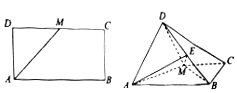
(1)求证:AD⊥BM;
(2)若点E是线段DB上的一动点,问点E在何位置时,二面角E﹣AM﹣D的余弦值为 ![]() .
.
【答案】
(1)证明:∵长方形ABCD中, ![]() ,
, ![]() ,M为DC的中点,
,M为DC的中点,
∴AM=BM=2,∴BM⊥AM.
∵平面ADM⊥平面ABCM,平面ADM∩平面ABCM=AM,BM平面ABCM,
∴BM⊥平面ADM,
∵AD平面ADM,∴AD⊥BM
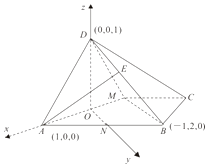
(2)证明:以O为原点,OA为x轴,ON为y轴,OD为z轴,
建立如图所示的直角坐标系
设 ![]() ,则平面AMD的一个法向量
,则平面AMD的一个法向量 ![]() ,
,
![]() =(1﹣λ,2λ,1﹣λ),
=(1﹣λ,2λ,1﹣λ), ![]() ,
,
设平面AME的一个法向量 ![]() ,
,
则  ,∴
,∴ ![]()
取y=1,得x=0,y=1, ![]() ,∴
,∴ ![]() ,
,
∵ ![]() =
= 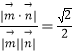 .∴得
.∴得 ![]() 或λ=﹣1,经检验得
或λ=﹣1,经检验得 ![]() 满足题意.
满足题意.
∴E为BD的三等分点.
【解析】(1)推导出BM⊥AM,从而BM⊥平面ADM,由此能证明AD⊥BM.(2)以O为原点,OA为x轴,ON为y轴,OD为z轴,建立空间直角坐标系,利用向量法能求出E为BD的三等分点.
【考点精析】关于本题考查的空间中直线与直线之间的位置关系,需要了解相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能得出正确答案.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】已知cos(π+α)= ![]() ,且
,且 ![]() <α<π.
<α<π.
(Ⅰ)求5sin(α+π)﹣4tan(3π﹣α)的值
(Ⅱ)若0<β< ![]() ,cos(β﹣α)=
,cos(β﹣α)= ![]() ,求sin(
,求sin( ![]() +2β)的值.
+2β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={1,2,3,4,5,6,7,8,9,10,11,12},以下命题正确的序号是 .
①如果函数f(x)=x(x﹣a1)(x﹣a2)…(x﹣a7),其中ai∈M(i=1,2,3,…,7),那么f′(0)的最大值为127 .
②数列{an}满足首项a1=2,ak+12﹣ak2=2,k∈N* , 当n∈M且n最大时,数列{an}有2048个.
③数列{an}(n=1,2,3,…,8)满足a1=5,a8=7,|ak+1﹣ak|=2,k∈N* , 如果数列{an}中的每一项都是集合M的元素,则符合这些条件的不同数列{an}一共有33个.
④已知直线amx+any+ak=0,其中am , an , ak∈M,而且am<an<ak , 则一共可以得到不同的直线196条.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E , F分别为棱AB , CC1的中点,则在平面ADD1A1内且与平面D1EF平行的直线( )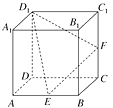
A.不存在
B.有1条
C.有2条
D.有无数条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,则P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com