[题目]如图.在正方体ABCD-A1B1C1D1中.E . F分别为棱AB . CC1的中点.则在平面ADD1A1内且与平面D1EF平行的直线( )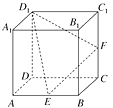A.不存在B.有1条C.有2条D.有无数条题目和参考答案——青夏教育精英家教网—

【题目】如图，在正方体ABCD－A1B1C1D1中，E ， F分别为棱AB ， CC1的中点，则在平面ADD1A1内且与平面D1EF平行的直线( )

A.不存在
B.有1条
C.有2条
D.有无数条

【答案】D
【解析】在上取一点，使得，连接，可证得，所以四点共面，所以在平面内，

平行于的直线均平行于平面，这样的直线有无数条，故D符合题意。
所以答案是D．

【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对直线与平面平行的性质的理解，了解一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行;简记为：线面平行则线线平行．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】由代数式的乘法法则类比推导向量的数量积的运算法则：
①mn=nm类比得到ab=ba；
②（m+n）t=mt+nt类比得到（a+b）c=ac+bc；
③（mn）t=m（nt）类比得到（ab）c=a（bc）；
④t≠0，mt=rtm=r类比得到p≠0，ap=bpa=b；
⑤|mn|=|m||n|类比得到|ab|=|a||b|；
⑥ = 类比得到．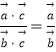
以上式子中，类比得到的结论正确的序号是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列{an}的前n项和为Sn ，且Sn+an=1，数列{bn}为等差数列，且b1+b2=b3=3．
（1）求Sn；
（2）求数列（anbn）的前n项和Tn ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上，记 =λ．当∠APC为锐角时，λ的取值范围是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知长方形ABCD中，AB=2 ，AD= ，M为DC的中点．将△ADM沿AM折起，使得平面ADM⊥平面ABCM．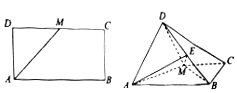
（1）求证：AD⊥BM；
（2）若点E是线段DB上的一动点，问点E在何位置时，二面角E﹣AM﹣D的余弦值为．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在空间四边形ABCD中，E ， F分别为AB ， AD上的点，且，H ， G分别为BC ， CD的中点，则( )

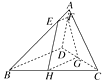
A.BD∥平面EFGH ，且四边形EFGH是平行四边形
B.EF∥平面BCD ，且四边形EFGH是梯形
C.HG∥平面ABD ，且四边形EFGH是平行四边形
D.EH∥平面ADC ，且四边形EFGH是梯形

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知三棱柱ABC-A′B′C′，底面是边长为1的正三角形，侧面为全等的矩形且高为8，求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.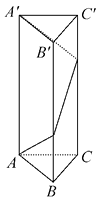

本题条件不变，求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】用数学归纳法证明12+22+…+（n﹣1）2+n2+（n﹣1）2+…+22+12═ 时，由n=k的假设到证明n=k+1时，等式左边应添加的式子是（）
A.（k+1）2+2k2
B.（k+1）2+k2
C.（k+1）2
D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：

使用年数	2	4	6	8	10
售价	16	13	9.5	7	4.5

（1）试求y关于x的回归直线方程；（参考公式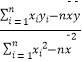： = ， =y﹣ ）
（2）已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？（利润=售价﹣收购价）

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学