
【题目】已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.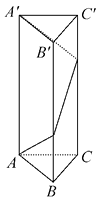
本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.
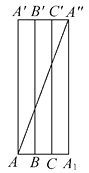
【答案】解:将三棱柱侧面沿侧棱AA′剪开,展成平面图形如图,则AA″即为所求的最短路线.
在Rt△AA1A″中,AA1=3,A1A″=8,所以AA″= ![]() =
= ![]() .
.
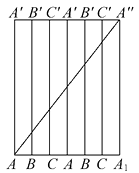
将两个相同的题目中的三棱柱的侧面都沿AA′剪开,然后展开并拼接成如图所示,则AA″即为所求的最短路线.在Rt△AA1A″中,AA1=6,A1A″=8,
所以AA″= ![]() =
= ![]() =10.
=10.
【解析】考察“最短路线长”一般是求几何体侧面展开图像的对角线的距离。根据已知条件结合勾股定理即可得出。
【考点精析】解答此题的关键在于理解棱柱的结构特征的相关知识,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


科目:高中数学 来源: 题型:
【题目】已知f(x)=(logmx)2+2logmx﹣3(m>0,且m≠1).
(Ⅰ)当m=2时,解不等式f(x)<0;
(Ⅱ)f(x)<0在[2,4]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,E , F分别为棱AB , CC1的中点,则在平面ADD1A1内且与平面D1EF平行的直线( )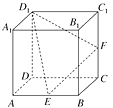
A.不存在
B.有1条
C.有2条
D.有无数条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为m与p,且乙投球3次均未命中的概率为 ![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率p;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式(ax+1)(ex﹣aex)≥0在(0,+∞)上恒成立,则实数a的取值范围是( )
A.(﹣∞,1]
B.[0,1]
C.![]()
D.[0,e]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com