
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将所得曲线C向右平移1个单位长度,再将曲线C上的所有点的横坐标变为原来的2倍,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线l的距离的最大值.
上的点到直线l的距离的最大值.
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.![]() 为
为![]() 的右焦点,
的右焦点,![]() 为
为![]() 上一点,
上一点,![]() 轴,
轴,![]() 的半径为
的半径为![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 交于
交于![]() 两点,与
两点,与![]() 交于
交于![]() 两点,其中
两点,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 轴为始边做两个锐角
轴为始边做两个锐角![]() ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]()

(1)求![]() 的值; (2)求
的值; (2)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为![]() ,且图象上一个最低点为
,且图象上一个最低点为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,且经过点
的长轴长为4,且经过点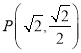 .
.
(1)求椭圆的方程;
(2)直线![]() 的斜率为
的斜率为![]() ,且与椭圆相交于
,且与椭圆相交于![]() ,
,![]() 两点(异于点
两点(异于点![]() ),过
),过![]() 作
作![]() 的角平分线交椭圆于另一点
的角平分线交椭圆于另一点![]() .
.
(i)证明:直线![]() 与坐标轴平行;
与坐标轴平行;
(ii)当![]() 时,求四边形
时,求四边形![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
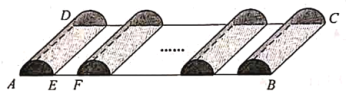
【题目】如图,某人承包了一块矩形土地![]() 用来种植草莓,其中
用来种植草莓,其中![]() m,
m,![]() m.现规划建造如图所示的半圆柱型塑料薄膜大棚
m.现规划建造如图所示的半圆柱型塑料薄膜大棚![]() 个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米
个,每个半圆柱型大棚的两半圆形底面与侧面都需蒙上塑料薄膜(接头处忽略不计),塑料薄膜的价格为每平方米![]() 元;另外,还需在每个大棚之间留下
元;另外,还需在每个大棚之间留下![]() m宽的空地用于建造排水沟与行走小路(如图中
m宽的空地用于建造排水沟与行走小路(如图中![]() m),这部分建设造价为每平方米
m),这部分建设造价为每平方米![]() 元.
元.
(1)当![]() 时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留
时,求蒙一个大棚所需塑料薄膜的面积;(本小题结果保留![]() )
)
(2)试确定大棚的个数,使得上述两项费用的和最低?(本小题计算中![]() 取
取![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于三次函数![]() ,给出定义:设
,给出定义:设![]() 是函数
是函数![]() 的导数,
的导数,![]() 是
是![]() 的导数,若方程
的导数,若方程![]() 有实数解
有实数解![]() ,则称点
,则称点![]() 为函数
为函数![]() 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com