
分析 设t=3x,由指数函数的单调性,可得t的范围,将方程化为k=$\frac{30}{{t}^{2}-3t+6}$在[1,9]有解,设f(t)=t2-3t+6,求出在[1,9]的值域,即可得到所求k的范围.
解答 解:设t=3x,由x∈[0,2],可得t∈[1,9],
方程k•9x-k•3x+1+6(k-5)=0,即为kt2-3kt+6(k-5)=0,
即k=$\frac{30}{{t}^{2}-3t+6}$在[1,9]有解,
由f(t)=t2-3t+6=(t-$\frac{3}{2}$)2+$\frac{15}{4}$,
当t=$\frac{3}{2}$∈[1,9]时,f(t)取得最小值$\frac{15}{4}$,
f(1)=4,f(9)=60,可得f(t)的最大值为60.
可得k的最小值为$\frac{30}{60}$=$\frac{1}{2}$,
k的最大值为$\frac{30}{\frac{15}{4}}$=8,
即有k的取值范围是[$\frac{1}{2}$,8].
点评 本题考查函数方程的转化思想,注意运用换元法和指数函数、二次函数的值域求法,考查化简整理的运算能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | $0<m≤\frac{1}{3}$ | B. | $0<m<\frac{1}{2}$ | C. | $\frac{1}{2}<m≤1$ | D. | $\frac{1}{3}<m<1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
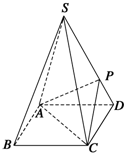 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,P为侧棱SD上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
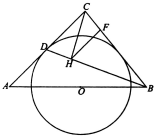 如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.
如图,等腰直角三角形ACB中,∠ACB=90°,圆心O为AB的中点,AC切圆O于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 态度 | 积极支持企业改革 | 不太支持企业改革 | 总计 |
| 工作积极 | 54 | 40 | 94 |
| 工作一般 | 32 | 63 | 95 |
| 总计 | 86 | 103 | 189 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{1}{4}$) | B. | (-$\frac{1}{4}$,-$\frac{1}{8}$) | C. | (-$\frac{1}{8}$,-$\frac{1}{16}$) | D. | (-$\frac{1}{16}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{-1}{x}$ | B. | y=$\left\{\begin{array}{l}{\sqrt{x},x≥0}\\{\sqrt{-x},x<0}\end{array}\right.$ | C. | y=ex+e-x | D. | y=-x|x| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com