
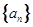 中,
中,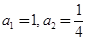 ,且
,且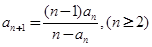 .
.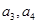 ,猜想
,猜想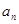 的表达式,并加以证明;
的表达式,并加以证明;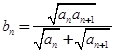 ,求证:对任意的自然数
,求证:对任意的自然数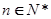 ,都有
,都有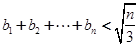 ;
;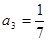 ,
,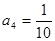 ;
; ,
,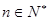 证明:见解析.
证明:见解析.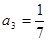 ,
,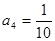 ----------------------(2分)
----------------------(2分) ,
,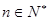 下面利用数学归纳法加以证明:
下面利用数学归纳法加以证明: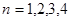 时,结论成立,-----------------(3分)
时,结论成立,-----------------(3分)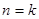 ;
; 时(也可以
时(也可以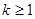 ),结论也成立,即
),结论也成立,即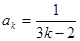 ,
,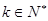 --------------------------(4分)
--------------------------(4分)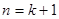 时,由题设与归纳假设可知:
时,由题设与归纳假设可知: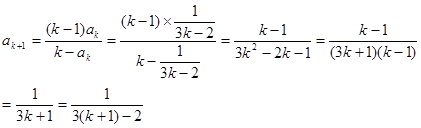 ------------(6分)
------------(6分)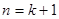 时,结论也成立,综上,对
时,结论也成立,综上,对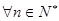 ,
, 成立。--------(7分)
成立。--------(7分)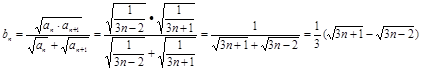 ---(9分)
---(9分)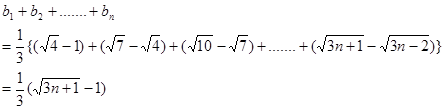 ---------(11分)
---------(11分)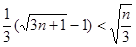
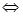
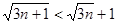
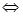
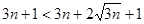
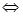
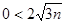 (显然成立)
(显然成立)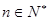 ,都有
,都有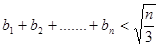 -------(14分)
-------(14分)

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源:不详 题型:填空题
 是等和数列,
是等和数列, =3,公和是5,则此数列的前805项的和为 .
=3,公和是5,则此数列的前805项的和为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.5 | B.6 | C.7 | D.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com