
 AB,∠ABC=60°,E为AB的中点.
AB,∠ABC=60°,E为AB的中点. 
 (Ⅰ)证明:在菱形ABCD中,∵∠ABC=60°
(Ⅰ)证明:在菱形ABCD中,∵∠ABC=60° ,EP=EA=EB=1,EC=
,EP=EA=EB=1,EC= ,
, ,0),P(0,0,1),D(-2,
,0),P(0,0,1),D(-2,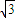 ,0)
,0) ,其中0≤k≤1,则
,其中0≤k≤1,则 ,
, 为平面PEC的法向量,
为平面PEC的法向量, ,得k=
,得k= ,
, ,
, )…(9分)
)…(9分) 为平面EFC的法向量,则
为平面EFC的法向量,则
 令z=2,得x=1,取
令z=2,得x=1,取 ,
, 为平面PBC的法向量,则
为平面PBC的法向量,则 得出
得出
 ,取
,取 ,
, )|=
)|= =
= …(12分)
…(12分)

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中数学 来源: 题型:
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD中,侧棱PA⊥平面ABCD,底面ABCD是平行四边形,PB=PC,AB=1,BC=
如图,已知四棱锥P-ABCD中,侧棱PA⊥平面ABCD,底面ABCD是平行四边形,PB=PC,AB=1,BC=| 2 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°;⑤直线PD与平面PAB所成角的余弦值为
| ||
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=
如图,已知圆O的直径AB长度为4,点D为线段AB上一点,且AD=| 1 |
| 3 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com