【答案】
分析:(1)由x=2是函数f(x)=(x
2+ax-2a-3)e
x的一个极值点可得到x=2是f′(x)=0的根,从而求出a
(2)研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值与最小值.
解答:解:(I)由f(x)=(x
2+ax-2a-3)e
x可得
f′(x)=(2x+a)e
x+(x
2+ax-2a-3)e
x=[x
2+(2+a)x-a-3]e
x(4分)
∵x=2是函数f(x)的一个极值点,
∴f′(2)=0
∴(a+5)e
2=0,解得a=-5(6分)
(II)由f′(x)=(x-2)(x-1)e
x>0,得f(x)在(-∞,1)递增,在(2,+∞)递增,
由f′(x)<0,得f(x)在在(1,2)递减
∴f(2)=e
2是f(x)在
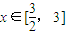
的最小值;(8分)
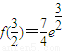
,f(3)=e
3
∵

∴最大值为e
3,最小值为e
2点评:本题考查了利用导数研究函数的极值,利用导数求闭区间上函数的最值,属于中档题.

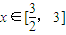 的最大值和最小值.
的最大值和最小值.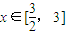 的最小值;(8分)
的最小值;(8分)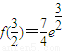 ,f(3)=e3
,f(3)=e3 ∴最大值为e3,最小值为e2
∴最大值为e3,最小值为e2
