
已知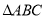 的角
的角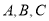 所对的边份别为
所对的边份别为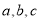 ,且
,且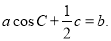
(1)求角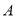 的大小;
的大小;
(2)若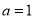 ,求
,求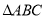 的周长
的周长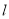 的取值范围.
的取值范围.
(1)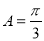 ;(2)
;(2) .
.
【解析】
试题分析:(1)利用正弦定理、三角形内角和定理及同角三角函数关系,将条件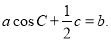 化为
化为
sinB=sin(A+C)=sinAcosC+cosAsinC,再利用两角和与差的三角函数公式化简,求得cosA=,从而确定角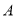 的大小;
的大小;
(2)由题设利用正弦定理将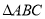 的周长
的周长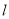 表示民关于角B的三角函数,然后利用三角函数的性质求周长
表示民关于角B的三角函数,然后利用三角函数的性质求周长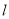 的取值范围.
的取值范围.
试题解析:【解析】
(1)由acosC+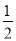 c=b和正弦定理得,
c=b和正弦定理得,
sinAcosC+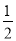 sinC=sinB,
sinC=sinB,
又sinB=sin(A+C)=sinAcosC+cosAsinC,
∴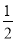 sinC=cosAsinC,
sinC=cosAsinC,
∵sinC≠0,∴cosA= ,
,
∵0<A<π,∴A=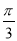 .
.
(2)由正弦定理得,b=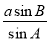 =
=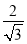 sinB,c=
sinB,c=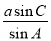 =
=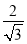 sinC,
sinC,
则l=a+b+c=1+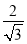 (sinB+sinC)
(sinB+sinC)
=1+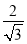 [sinB+sin(A+B)]
[sinB+sin(A+B)]
=1+2(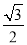 sinB+
sinB+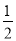 cosB)=1+2sin(B+
cosB)=1+2sin(B+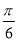 ).
).
∵A=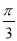 ,∴B∈(0,
,∴B∈(0,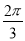 ),∴B+
),∴B+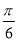 ∈(
∈(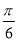 ,
,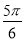 ),
),
∴sin(B+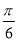 )∈(
)∈(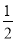 ,1],
,1],
∴△ABC的周长l的取值范围为(2,3].
考点:1、正弦定理;2、三角函数的性质;3、同角三角函数的基本关系;4、两角和与差的三角函数.


科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考理科数学试卷(解析版) 题型:选择题
在边长为1的正三角形ABC中, =x
=x ,
,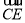 =y
=y ,x>0,y>0,且x+y=1,
,x>0,y>0,且x+y=1,
则 ·
· 的最大值为 ( )
的最大值为 ( )
A.- B.-
B.-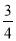 C.-
C.- D.-
D.-
查看答案和解析>>
科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考文科数学试卷(解析版) 题型:填空题
已知定义在R上的可导函数y=f(x)的图象在点M(1,f(1))处的切线方程为y=-x+2,则f(1)+f ′(1)=________.
查看答案和解析>>
科目:高中数学 来源:2015届湖南省娄底市名校高三9月联考文科数学试卷(解析版) 题型:选择题
若函数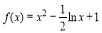 在其定义域内的一个子区间
在其定义域内的一个子区间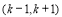 内不是单调函数,则实数k的取值范围 ( )
内不是单调函数,则实数k的取值范围 ( )
A.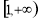 B.
B.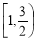 C.
C.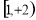 D.
D.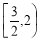
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com