
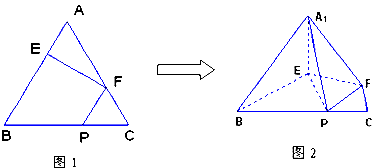
| 解:不妨设正三角形ABC的边长为3。 (1)在图1中,取BE的中点D,连结DF。 ∵AE:EB=CF:FA=1:2, ∵AF=AD=2,而∠A=60°, ∴△ADF是正三角形。 又AE=DE=1, ∴EF⊥AD 在图2中,A1E⊥EF,BE⊥EF, ∴∠A1EB为二面角A1-EF-B的平面角。 由题设条件知此二面角为直二面角, ∴A1E⊥BE。 又BE∩EF=E, ∴A1E⊥平面BEF,即A1E⊥平面BEP。 (2)在图2中,∵A1E不垂直于A1B, ∴A1E是平面A1BP的斜线。 又A1E⊥平面BEP, ∴A1E⊥BP, 从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理)。 设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q, 则∠EA1Q就是A1E与平面A1BP所成的角,且BP⊥A1Q。 在△EBP中,∵BE=BP=2,∠EBP=60°, ∴△EBP是等边三角形, ∴BE=EP 又A1E⊥平面BEP, ∴A1B=A1P, ∴Q为BP的中点,且 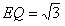 。 。又A1E=1, 在Rt△A1EQ中, 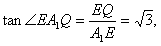 ∴∠EA1Q=60° 所以直线A1E与平面A1BP所成的角为60°。 |
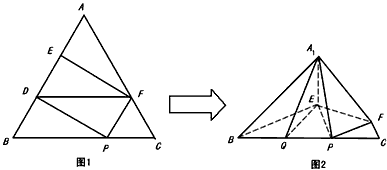 |
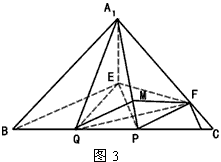
| (3)在图3中,过F作FM⊥A1P于M,连结QM,QF。 ∵CF=CP=1,∠C=60°, ∴△FCP是正三角形, ∴PF=1 又 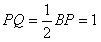 ∴PF=PQ。 ① ∵A1E⊥平面BEP, 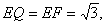 ∴A1F=A1Q; ∴△A1FP≌△A1QP 从而∠A1PF=∠A1PQ ② 由①②及MP为公共边知△FMP≌△QMP, ∴∠QMP=∠FMP=90°,且MF=MQ, 从而∠FMQ为二面角B-A1P-F的平面角。 在Rt△A1QP中,A1Q=A1F=2,PQ=1, ∴ 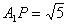 ∵MQ⊥A1P ∴  ∴ 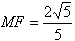 在△FCQ中,FC=1,QC=2,∠C=60°, 由余弦定理得QF= 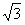 。 。在△FMQ中 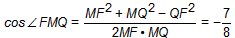 ∴二面角B-A1P-F的大小为 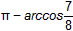 。 。 |
 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
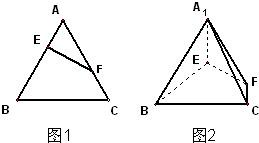 在正三角形ABC中,E、F分别是AB、AC边上的点,满足
在正三角形ABC中,E、F分别是AB、AC边上的点,满足| AE |
| EB |
| CF |
| FA |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com