
| x | 2 | 3 | 4 | 5 | 6 |
| y | 1.4 | 2.3 | 3.1 | 3.7 | 4.5 |
 考前必练系列答案
考前必练系列答案科目:高中数学 来源:不详 题型:解答题
 次预赛成绩记录如下:
次预赛成绩记录如下: 


 乙
乙 


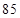
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,第2组
,第2组 ,第3组
,第3组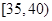 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

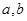 的值;
的值;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 有关.
有关.  是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.
是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.  日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:
日均值越小,空气质量越好. 2012年2月29日,国家环保部发布的《环境空气质量标准》见下表:  日均值k(微克) 日均值k(微克) | 空气质量等级 |
 | 一级 |
 | 二级 |
 | 超标 |
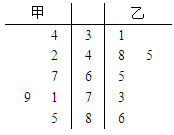
 日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市
日均值作为样本,样本数据茎叶图如上右图所示(十位为茎,个位为叶). (Ⅰ)分别求出甲、乙两市 日均值的样本平均数,并由此判断哪个市的空气质量较好;
日均值的样本平均数,并由此判断哪个市的空气质量较好;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
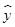 =0.50x-0.81,则x=25时,
=0.50x-0.81,则x=25时,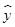 为11.69
为11.69查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| | 黑 | 红 |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
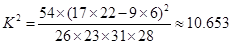 ,因为
,因为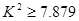 ,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为_ .
,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为_ .查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.1,2,3,4,5 | B.2,4,6,8,10 |
| C.5,16,27,38,49 | D.4,13,22,31,40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com