
设函数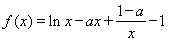 .
.
(Ⅰ)当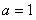 时,求曲线
时,求曲线 在
在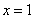 处的切线方程;
处的切线方程;
(Ⅱ)当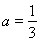 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅲ)在(Ⅱ)的条件下,设函数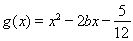 ,若对于
,若对于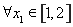 ,
,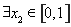 ,使
,使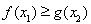 成立,求实数
成立,求实数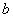 的取值范围.
的取值范围.
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十五选修4-2第二节练习卷(解析版) 题型:解答题
已知M=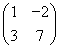 .
.
(1)求逆矩阵M-1.
(2)若向量X满足MX=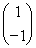 ,试求向量X.
,试求向量X.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十三第十章第十节练习卷(解析版) 题型:选择题
在调查学生数学成绩与物理成绩之间的关系时,得到如下数据(人数):
| 物理 成绩好 | 物理 成绩不好 | 合计 |
数学成绩好 | 62 | 23 | 85 |
数学成绩不好 | 28 | 22 | 50 |
合计 | 90 | 45 | 135 |
那么有把握认为数学成绩与物理成绩之间有关的百分比为( )
(A)25% (B)75% (C)95% (D)99%
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:解答题
某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是 ,
, ,
, 且各轮次通过与否相互独立.
且各轮次通过与否相互独立.
(1)设该选手参赛的轮次为ξ,求ξ的分布列.
(2)对于(1)中的ξ,设“函数f(x)=3sin π(x∈R)是偶函数”为事件D,求事件D发生的概率.
π(x∈R)是偶函数”为事件D,求事件D发生的概率.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十一第十章第八节练习卷(解析版) 题型:选择题
设某项试验的成功率是失败率的2倍,用随机变量X去描述1次试验的成功次数,则P(X=0)等于( )
(A)0 (B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知向量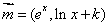 ,
,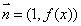 ,
,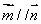 (
(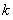 为常数,
为常数, 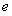 是自然对数的底数),曲线
是自然对数的底数),曲线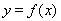 在点
在点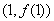 处的切线与
处的切线与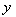 轴垂直,
轴垂直,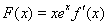 .
.
(Ⅰ)求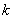 的值及
的值及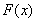 的单调区间;
的单调区间;
(Ⅱ)已知函数 (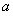 为正实数),若对于任意
为正实数),若对于任意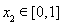 ,总存在
,总存在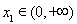 , 使得
, 使得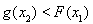 ,求实数
,求实数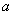 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
若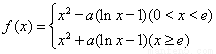 ,其中
,其中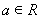 .
.
(1)当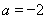 时,求函数
时,求函数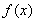 在区间
在区间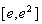 上的最大值;
上的最大值;
(2)当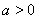 时,若
时,若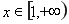 ,
,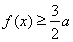 恒成立,求
恒成立,求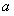 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:填空题
设命题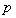 :实数
:实数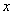 满足
满足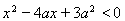 ,其中
,其中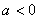 ;命题
;命题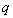 :实数
:实数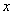 满足
满足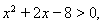 且
且 的必要不充分条件,则实数
的必要不充分条件,则实数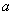 的取值范围是 .
的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com