【题目】某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
（1）求回归直线方程
＝bx＋a，其中b＝－20，a＝－b
（2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润＝销售收入—成本）
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
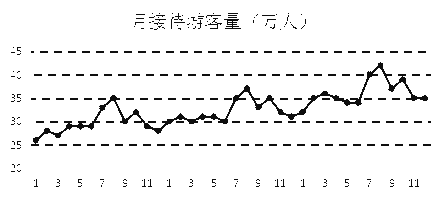
2014年 2015年 2016年
根据该折线图，下列结论错误的是( )
A. 年接待游客量逐年增加
B. 月接待游客量逐月增加
C. 各年的月接待游客量高峰期大致在7，8月
D. 各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
的定义域是R，对于任意实数
，恒有
，且当
时， 
。
（1）求证： 
，且当
时，有
；
（2）判断
在R上的单调性；
（3）设集合A＝
，B＝
，若A∩B＝
，求
的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱是AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，设BM=x，x∈[0，1]，给出以下四种说法：
（1）平面MENF⊥平面BDD′B′；
（2）当且仅当x=
时，四边形MENF的面积最小；
（3）四边形MENF周长L=f（x），x∈[0，1]是单调函数；
（4）四棱锥C′﹣MENF的体积V=h（x）为常函数，以上说法中正确的为（ ）
A. （2）（3） B. （1）（3）（4） C. （1）（2）（4） D. （1）（2）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，C、D是以AB为直径的圆上两点，AB=2AD=2
，AC=BC，F 是AB上一点，且AF=
AB，将圆沿直径AB折起，使点C在平面ABD的射影E在BD上，已知：
, 
（1）求证：AD⊥平面BCE；
（2）求三棱锥A﹣CFD的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2017全国Ⅱ,文19)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:
旧养殖法
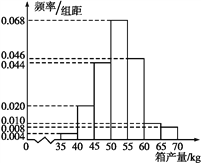
新养殖法
(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关;
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
,
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知菱形ABCD的边长为6，∠ABD=30°，点E、F分别在边BC、DC上，BC=2BE，CD=λCF．若 
=﹣9，则λ的值为（ ）
A.2
B.3
C.4
D.5
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f1(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<
)的一段图象过点(0,1)，如图所示．
(1)求函数f1(x)的表达式；
(2)将函数y＝f1(x)的图象向右平移
个单位，得函数y＝f2(x)的图象，求y＝f2(x)的最大值，并求出此时自变量x的集合．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
