
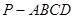 中,四边形
中,四边形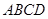 为正方形,
为正方形,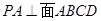 ,且
,且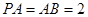 ,
,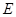 为
为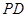 中点.
中点.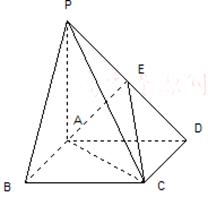
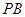 //平面
//平面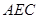 ;
;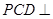 平面
平面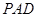 ;
;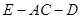 的正弦值.
的正弦值.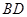 交
交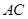 于点
于点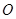 ,连结
,连结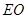 ,那么根据中位线性质可知
,那么根据中位线性质可知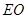 //
//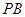 ,那么结合线面平行的判定定理来得到。
,那么结合线面平行的判定定理来得到。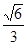
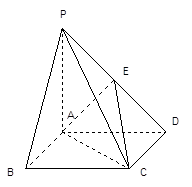
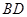 交
交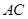 于点
于点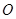 ,连结
,连结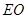 ……………………1分
……………………1分
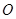 为
为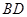 中点,
中点,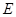 为
为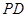 中点,
中点,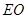 //
//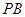 ……………………2分
……………………2分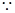
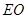
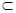 平面
平面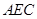 ,
,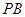
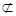 平面
平面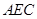 , ………3分
, ………3分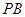 //平面
//平面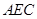 .
. 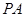 ⊥平面
⊥平面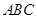
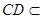 平面
平面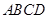 ,
,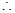
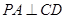 . …………4分
. …………4分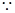 在正方形
在正方形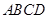 中
中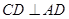 且
且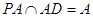 , …5分
, …5分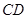
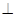 平面
平面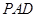 . ……………………6分
. ……………………6分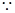
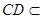 平面
平面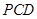 ,
,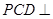 平面
平面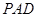 . ……………………7分
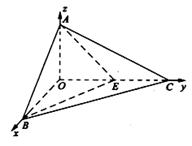
. ……………………7分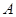 为坐标原点,
为坐标原点,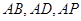 所在直线分别为
所在直线分别为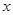 轴,
轴,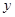 轴,
轴,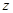 轴建立空
轴建立空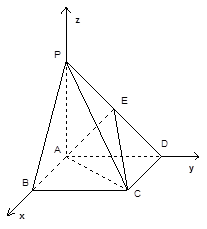
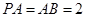 可知
可知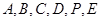 的坐标分别为
的坐标分别为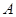 (0, 0, 0),
(0, 0, 0), 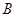 (2, 0, 0),
(2, 0, 0),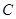 (2, 2, 0),
(2, 2, 0), 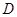 (0, 2, 0),
(0, 2, 0), 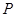 (0, 0, 2),
(0, 0, 2), 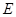 (0, 1, 1) .………9分
(0, 1, 1) .………9分
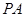
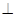 平面
平面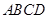 ,∴
,∴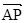 是平面
是平面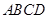 的法向量,
的法向量,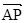 =(0, 0, 2).
=(0, 0, 2).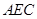 的法向量为
的法向量为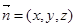 ,
, 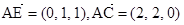 ,
, 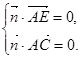 即
即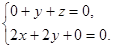
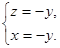
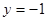 ,则
,则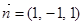 . ………………11分
. ………………11分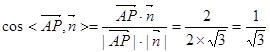 ,
, 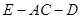 的正弦值为
的正弦值为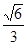 …………………12分
…………………12分

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:不详 题型:解答题
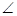 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.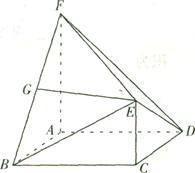
 面ABF;
面ABF;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
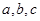 ,若
,若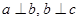 ,则
,则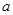 ∥
∥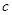 ;②
;②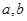 是异面直线,
是异面直线,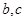 是异面直线,则
是异面直线,则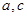 不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面
不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面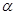 垂直;④平面
垂直;④平面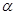 //平面
//平面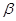 ,点
,点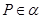 ,直线
,直线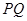 //
//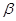 ,则
,则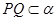 ;其中正确的命题的个数有( )
;其中正确的命题的个数有( )| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com