
已知三棱锥O-ABC中,OA、OB、OC两两垂直,OC=1,OA=x,OB=y,若x+y=4,则三棱锥体积的最大值是( )
A.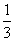 B.
B.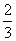
C.1 D.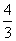
科目:高中数学 来源: 题型:
已知a,b是两条不同的直线,α,β,γ是三个不同的平面,下列命题中:
①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;
②若a,b相交,且都在α,β外,a∥α,a∥β,b∥α,b∥β,则α∥β;
③若α⊥β,α∩β=a,bβ,a⊥b,则b⊥α;
④若aα,bα,l⊥a,l⊥b,则l⊥α.其中正确命题的序号是( )
A.①②③ B.①③
C.②③ D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
PA垂直于正方形ABCD所在平面,连接PB,PC,PD,AC,BD,则下列垂直关系正确的是( )
①面PAB⊥面PBC ②面PAB⊥面PAD
③面PAB⊥面PCD ④面PAB⊥面PAC
A.①② B.①③
C.②③ D.②④

查看答案和解析>>
科目:高中数学 来源: 题型:
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥侧面积和体积分别是( )

A.4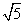 ,8 B.4
,8 B.4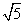 ,
,
C.4(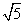 +1),
+1), D.8,8
D.8,8
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A(2,5,-6),点P在y轴上,|PA|=7,则点P的坐标是( )
A.(0,8,0) B.(0,2,0)
C.(0,8,0)或(0,2,0) D.(0,-8,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l: kx-y+1+2k=0(k∈R).
(1)证明:直线l过定点;
(2)若直线不经过第四象限,求k的取值范围;
(3)若直线l交x轴负半轴于A,交y轴正半轴于B,△AOB的面积为S,求S的最小值并求此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com