
分析 (1)由椭圆的通径公式,及椭圆的性质a2=b2+1,即可求得a和b的值,求得椭圆方程;
(2)设直线l的方程,代入椭圆方程,利用韦达定理,及直线的斜率公式,即可求得m与k的关系,代入直线方程,即可求得直线恒过定点;当直线l的斜率不存在时,根据斜率公式,即可求得直线l的方程,即可证明直线AB过定点.
解答 解:(1)由已知得c=2,丨PQ丨=$\frac{2{b}^{2}}{a}$=2$\sqrt{2}$,即$\sqrt{2}$a=b2,①
由a2=b2+c2=b2+1,②
由①②解得:b=2,a=2$\sqrt{2}$
故椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;
(2)证明:若直线AB的斜率存在,设AB方程为y=kx+m,且m≠±2,设A(x1,y1),B(x2,y2),
$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,整理得:(2k2+1)x2+4kmx+2m2-8=0,
x1+x2=-$\frac{4{k}^{2}}{2{k}^{2}+1}$,x1x2=$\frac{2{m}^{2}-8}{2{k}^{2}+1}$,
由已知可知:$\frac{{y}_{1}-2}{{x}_{1}}$+$\frac{{y}_{2}-2}{{x}_{2}}$=8,
则$\frac{k{x}_{1}+m-2}{{x}_{1}}$+$\frac{k{x}_{2}+m-2}{{x}_{2}}$=8,
即2k+(m-2)$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=8,…(8分)
∴k-$\frac{mk}{m+2}$=4,整理得m=$\frac{1}{2}$k-2.
故直线AV的方程为y=kx+$\frac{1}{2}$k-2,即y=k(x+$\frac{1}{2}$)-2.
所以直线AB过定点(-$\frac{1}{2}$,-2). …(10分)
若直线AB的斜率不存在,设AB方程为x=x0,
设A(x0,y0),B(x0,-y0),
由已知$\frac{{{y_0}-2}}{x_0}+\frac{{-{y_0}-2}}{x_0}=8$,
得${x_0}=-\frac{1}{2}$.此时AB方程为$x=-\frac{1}{2}$,显然过点(-$\frac{1}{2}$,-2).
综上,直线AB过定点(-$\frac{1}{2}$,-2).…(12分)
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{3}{4}$π) | B. | ($\frac{π}{3}$,$\frac{3}{4}$π] | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{3}{4}$π)∪($\frac{π}{4}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
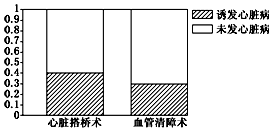
| A. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的 | |
| B. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同 | |
| C. | 此等高条形图看不出两种手术有什么不同的地方 | |
| D. | “心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com