
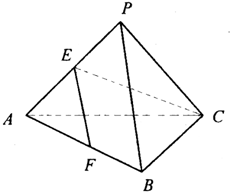
 在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.
在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.分析 (1)证明EF∥PB,然后利用直线与平面平行的判定定理证明直线PB∥平面EFC.
(2)取棱AC的中点为D,连接PD,BD证明AC⊥PB,推出AC⊥EF,然后证明EF⊥平面PAC,即可证明面PAC⊥平面PAB.
解答 (本小题满分10分)
证明:(1)∵E,F分别为棱PA、AB的中点,∴EF∥PB…(1分)
∵EF?平面EFC,PB?平面EFC…(2分)
∴直线PB∥平面EFC;…(3分)
(2)取棱AC的中点为D,连接PD,BD,…(4分)
∵三棱锥P-ABC是正三棱锥,∴PA=PC,BA=BC,
∴PD⊥AC,BD⊥AC∵PD∩BD=D,
∴AC⊥平面PDB∵PB?平面PDB,∴AC⊥PB…(7分)
由(1)知EF∥PB,∴AC⊥EF,
∵EF⊥CE,CE∩AC=C,AC?平面PAC,CE?平面PAC,
∴EF⊥平面PAC,…(9分)
∵EF?平面PAB,
∴平面PAC⊥平面PAB…(10分)
点评 本题排除直线与平面平行的判定定理以及平面与平面垂直的判定定理的应用,考查空间想象能力以及逻辑推理能力.


科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,${2^{x_0}}$>0 | B. | ?x0∈R,${2^{x_0}}$<0 | C. | ?x∈R,2x≤0 | D. | ?x0∈R,${2^{x_0}}$≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | -3$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com