
分析 (1)利用an,an+1是关于x的方程x2-2n•x+A=0(n∈N*)的两实根,可得an+an+1=2n,整理变形可得数列{an-$\frac{1}{3}$x2n}是等比数列;
(2)根据对数的运算性质和裂项求和和放缩法即可证明.
解答 解:(Ⅰ)∵an,an+1是关于x的方程x2-2nx+A=0,(n∈N*)的两根,∴an+an+1=2n,
∴an+1-$\frac{1}{3}$×2n+1=-(an-${\;}^{\frac{1}{3}}$•2n),
∵a1=1,
∴a1-${\;}^{\frac{1}{3}}$•21=$\frac{1}{3}$
∴{an-${\;}^{\frac{1}{3}}$•2n}是$\frac{1}{3}$为首项,以-1为等比的等比数列;
(2)证明:由(1)可得an-${\;}^{\frac{1}{3}}$•2n=$\frac{1}{3}$(-1)n-1,
∴an=$\frac{1}{3}$[2n-(-1)n],
∴3an+(-1)n]=2n,
∴bn=n,
∴$\frac{1}{{b}_{n}({b}_{n}+2)}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)
∴$\frac{1}{{{b_1}({b_1}+2)}}+\frac{1}{{{b_2}({b_2}+2)}}+…+$$\frac{1}{{b}_{n}({b}_{n}+2)}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+($\frac{1}{n}$-$\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)<$\frac{3}{4}$.
点评 本题主要考查等比关系的确定、数列的求和等基础知识,考查运算求解能力.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
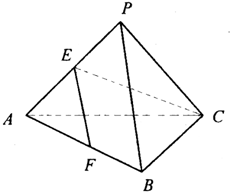 在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.
在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com