
分析 (1)利用已知条件通过赋值法求解即可.
(2)利用函数的单调性的定义判断证明即可.
(3)利用已知条件化简表达式为已知条件的形式,通过函数的单调性的性质化简求解即可.
解答 解:(1)令m=n=0得f(0)=1,令$m=\frac{1}{2},n=-\frac{1}{2}$,则$f(0)=f(-\frac{1}{2})+f(\frac{1}{2})-1$,
得$f(-\frac{1}{2})=0$,
(2)设x2>x1,则$f({x_2})-f({x_1})=f({x_2}-{x_1})-1=f[({x_2}-{x_1}-\frac{1}{2})+\frac{1}{2}]-1$=$[f({x_2}-{x_1}-\frac{1}{2})+f(\frac{1}{2})-1]-1=f({x_2}-{x_1}-\frac{1}{2})$,
因为x2>x1,所以${x_2}-{x_1}-\frac{1}{2}>0$,由已知当$x>-\frac{1}{2}$时有f(x)>0,
所以$f({x_2}-{x_1}-\frac{1}{2})>0$,
所以f(x2)>f(x1)所以f(x)在R上单调递增.
(3)原不等式等价于f(x2+1)≤f(1)+f(2|x|)-1=f(1+2|x|),
由(2)知f(x)在R上单调递增.
所以x2+1≤1+2|x|?|x|2+1≤1+2|x|,
解得0≤|x|≤2即-2≤x≤2,
所以原不等式解集为{x|-2≤x≤2}.
点评 本题考查抽象函数的应用,函数在求法,单调性的判断与证明,考查计算能力.


 核心素养学练评系列答案
核心素养学练评系列答案科目:高中数学 来源: 题型:解答题
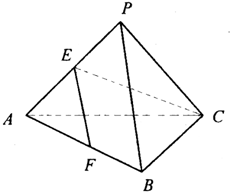 在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.
在正三棱锥P-ABC中,E、F分别为棱PA、AB的中点,且EF⊥CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±1 | B. | 1 | C. | ±2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com