
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
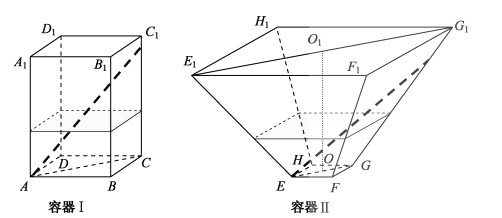
【答案】(1)16cm.(2)20cm.
【解析】
试题(1)转化为直角三角形ACM中,利用相似性质求解AP1;(2)转化到三角形EGN中,先利用直角梯形性质求角![]() ,再利用正弦定理求角
,再利用正弦定理求角![]() ,最后根据直角三角形求高,即为
,最后根据直角三角形求高,即为![]() 没入水中部分的长度.
没入水中部分的长度.
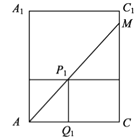
试题解析:解:(1)由正棱柱的定义,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,![]() .
.
记玻璃棒的另一端落在![]() 上点
上点![]() 处.
处.
因为![]() ,
,
所以![]() ,从而
,从而 ![]() ,
,
记![]() 与水面的焦点为
与水面的焦点为![]() ,过
,过![]() 作P1Q1⊥AC, Q1为垂足,
作P1Q1⊥AC, Q1为垂足,
则 P1Q1⊥平面 ABCD,故P1Q1=12,
从而 AP1= ![]() .
.
答:玻璃棒l没入水中部分的长度为16cm.
( 如果将“没入水中部分冶理解为“水面以上部分冶,则结果为24cm)
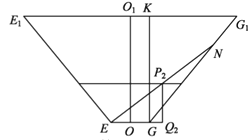
(2)如图,O,O1是正棱台的两底面中心.
由正棱台的定义,OO1⊥平面 EFGH, 所以平面E1EGG1⊥平面EFGH,O1O⊥EG.
同理,平面 E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.
记玻璃棒的另一端落在GG1上点N处.学科&网
过G作GK⊥E1G,K为垂足, 则GK =OO1=32.
因为EG = 14,E1G1= 62,
所以KG1= ![]() ,从而
,从而![]() .
.
设![]() 则
则![]() .
.
因为![]() ,所以
,所以![]() .
.
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() .
.
于是![]() .
.
记EN与水面的交点为P2,过 P2作P2Q2⊥EG,Q2为垂足,则 P2Q2⊥平面 EFGH,故P2Q2=12,从而 EP2=![]() .
.
答:玻璃棒l没入水中部分的长度为20cm.
(如果将“没入水中部分冶理解为“水面以上部分冶,则结果为20cm)


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为:
的方程为:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为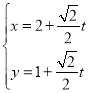 (
(![]() 为参数).
为参数).
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求
两点,求![]() 的值,并求定点
的值,并求定点![]() 到
到![]() 两点的距离之积.
两点的距离之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
(1)求实数k的值,并讨论函数f(x)的单调性;
(2)设函数g(x)![]() ,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某公园有三条观光大道![]() 围成直角三角形,其中直角边
围成直角三角形,其中直角边![]() ,斜边
,斜边![]() .现有甲、乙、丙三位小朋友分别在
.现有甲、乙、丙三位小朋友分别在![]() 大道上嬉戏,所在位置分别记为点
大道上嬉戏,所在位置分别记为点![]() .
.
(1)若甲乙都以每分钟![]() 的速度从点
的速度从点![]() 出发在各自的大道上奔走,到大道的另一端
出发在各自的大道上奔走,到大道的另一端
时即停,乙比甲迟2分钟出发,当乙出发1分钟后,求此时甲乙两人之间的距离;
(2)设![]() ,乙丙之间的距离是甲乙之间距离的2倍,且
,乙丙之间的距离是甲乙之间距离的2倍,且![]() ,请将甲
,请将甲
乙之间的距离![]() 表示为θ的函数,并求甲乙之间的最小距离.
表示为θ的函数,并求甲乙之间的最小距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1 km处,tan∠BAN=![]() ,∠BCN=
,∠BCN=![]() ,.现计划铺设一条电缆连通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元km、4万元km.
,.现计划铺设一条电缆连通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元km、4万元km.
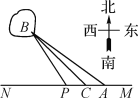
(1)求A,B两镇间的距离;
(2)应该如何铺设,使总铺设费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校健康社团为调查本校大学生每周运动的时长,随机选取了80名学生,调查他们每周运动的总时长(单位:小时),按照![]()
![]()
![]()
![]()
![]()
![]() 共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
共6组进行统计,得到男生、女生每周运动的时长的统计如下(表1、2),规定每周运动15小时以上(含15小时)的称为“运动合格者”,其中每周运动25小时以上(含25小时)的称为“运动达人”.
表1:男生
时长 |
|
|
|
|
|
|
人数 | 2 | 8 | 16 | 8 | 4 | 2 |
表2:女生
时长 |
|
|
|
|
|
|
人数 | 0 | 4 | 12 | 12 | 8 | 4 |
(1)从每周运动时长不小于20小时的男生中随机选取2人,求选到“运动达人”的概率;
(2)根据题目条件,完成下面![]() 列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
列联表,并判断能否有99%的把握认为本校大学生是否为“运动合格者”与性别有关.
每周运动的时长小于15小时 | 每周运动的时长不小于15小时 | 总计 | |
男生 | |||
女生 | |||
总计 | |||
参考公式: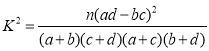 ,其中
,其中![]() .
.
参考数据:
| 0.40 | 0.25 | 0.10 | 0.010 |
| 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点焦点在x轴上,椭圆C上一点A(2![]() ,﹣1)到两焦点距离之和为8.若点B是椭圆C的上顶点,点P,Q是椭圆C上异于点B的任意两点.
,﹣1)到两焦点距离之和为8.若点B是椭圆C的上顶点,点P,Q是椭圆C上异于点B的任意两点.
(1)求椭圆C的方程;
(2)若BP⊥BQ,且满足3![]() 2
2![]() 的点D在y轴上,求直线BP的方程;
的点D在y轴上,求直线BP的方程;
(3)若直线BP与BQ的斜率乘积为常数λ(λ<0),试判断直线PQ是否经过定点.若经过定点,请求出定点坐标;若不经过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.
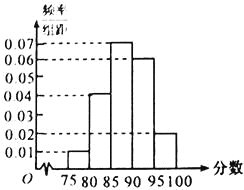
(1)下表是这次抽查成绩的频数分布表,试求正整数![]() 、
、![]() 的值;
的值;
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 50 | a | 350 | 300 | b |
(2)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求抽取成绩为优秀的学生人数;
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com