练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

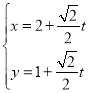    【题目】在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的方程为：，过点的直线的参数方程为（为参数）.

    （1）求直线的普通方程与曲线的直角坐标方程；

    （2）若直线与曲线交于、两点，求的值，并求定点到两点的距离之积.

    【答案】（1），（2），

    【解析】

    （1）利用消参法可得直线的普通方程，根据互化公式可得曲线的直角坐标方程；

    （2）将直线的参数方程代入曲线的方程，利用参数的几何意义化简计算即可.

    （1）由（为参数），消去参数，得直线的普通方程，

    由，即，得曲线的直角坐标方程为.

    （2）将直线的参数方程代入曲线的直角坐标方程中，得

    ，整理得，则，，

    由题意，，

    定点到，两点的距离之积为.

    所以，的值为，定点到，两点的距离之积.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，下列说法正确的是__________.的值域是；当时，方程有两个不等实根；若函数有三个零点时，则；经过有三条直线与相切.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂的某种产品成箱包装，每箱200件，每一箱产品在交付用户之前要对产品作检验，如检验出不合格品，则更换为合格品．检验时，先从这箱产品中任取20件作检验，再根据检验结果决定是否对余下的所有产品作检验，设每件产品为不合格品的概率都为，且各件产品是否为不合格品相互独立．

    （1）记20件产品中恰有2件不合格品的概率为,求的最大值点．

    （2）现对一箱产品检验了20件，结果恰有2件不合格品，以（1）中确定的作为的值．已知每件产品的检验费用为2元，若有不合格品进入用户手中，则工厂要对每件不合格品支付25元的赔偿费用．

    （i）若不对该箱余下的产品作检验，这一箱产品的检验费用与赔偿费用的和记为，求;

    （ii）以检验费用与赔偿费用和的期望值为决策依据，是否该对这箱余下的所有产品作检验？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四边形是直角梯形，，，，，为线段的中点，平面，，是线段的中点.

    （1）求证：∥平面；

    （2）求直线与平面所成的角的大小；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （Ⅰ）求直线的普通方程和曲线的直角坐标方程；

    （Ⅱ）设为曲线上的点，，垂足为，若的最小值为，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】 已知函数f(x)＝|x＋a|＋|x－2|.

    (1)当a＝－3时，求不等式f(x)≥3的解集；

    (2)若f(x)≤|x－4|的解集包含[1，2]，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列的定义为:在一个数列中，从第二项起,如果每一项与它的前一项的差都为同一个常数，那么这个数叫做等差数列，这个常数叫做该数列的公差．类比等差数列的定义给出“等和数列”的定义：_____________________________________；已知数列是等和数列，且，公和为，那么的值为____________．这个数列的前项和的计算公式为_____________________________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列：，，，…，为1，2，3，…，的一个排列，若互不相同，则称数列具有性质.

    （1）若，且，写出具有性质的所有数列；

    （2）若数列具有性质，证明：；

    （3）当时，分别判断是否存在具有性质的数列？请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

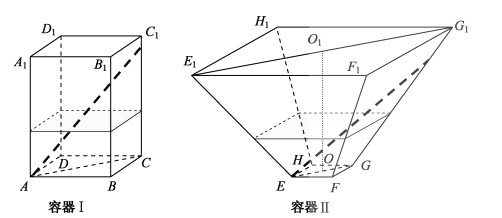
    【题目】如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm. 现有一根玻璃棒l，其长度为40cm.（容器厚度、玻璃棒粗细均忽略不计）

    （1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；

    （2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度.

    查看答案和解析>>

    同步练习册答案