
已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α= ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为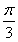 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.
(1)最小值为-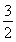 ,相应x的值为
,相应x的值为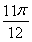 (2)-
(2)-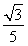
【解析】(1)∵b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),α=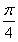 ,
,
∴f(x)=b·c=cos xsin x+2cos xsin α+sin xcos x+2sin xcos α=2sin xcos x+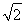 (sin x+cos x).
(sin x+cos x).
令t=sin x+cos x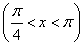 ,则2sin xcos x=t2-1,且-1<t<
,则2sin xcos x=t2-1,且-1<t<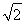 .
.
则y=t2+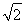 t-1=
t-1= 2-
2-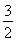 ,-1<t<
,-1<t<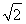 ,
,
∴t=-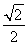 时,ymin=-
时,ymin=-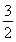 ,此时sin x+cos x=-
,此时sin x+cos x=-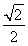 ,即
,即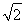 sin
sin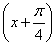 =-
=-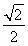 ,
,
∵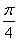 <x<π,∴
<x<π,∴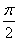 <x+
<x+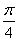 <
<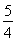 π,∴x+
π,∴x+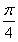 =
=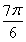 ,∴x=
,∴x=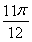 .
.
∴函数f(x)的最小值为-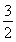 ,相应x的值为
,相应x的值为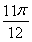 .
.
(2)∵a与b的夹角为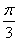 ,∴cos
,∴cos 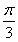 =
=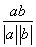 =cos αcos x+sin αsin x=cos(x-α).
=cos αcos x+sin αsin x=cos(x-α).
∵0<α<x<π,∴0<x-α<π,∴x-α=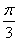 .
.
∵a⊥c,∴cos α(sin x+2sin α)+sin α(cos x+2cos α)=0,
∴sin(x+α)+2sin 2α=0,即sin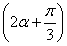 +2sin 2α=0,
+2sin 2α=0,
∴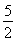 sin 2α+
sin 2α+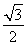 cos 2α=0,∴tan 2α=-
cos 2α=0,∴tan 2α=-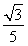 .
.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:选择题
双曲线x2-my2=1的实轴长是虚轴长的2倍,则m= ( )
A. 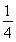 B.
B. 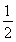 C.2 D.4
C.2 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:选择题
一个简单几何体的主视图、俯视图如图所示,则其左视图不可能为( )
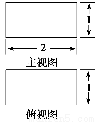
A.正方形 B.圆
C.等腰三角形 D.直角梯形
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(解析版) 题型:解答题
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xk,…;y1,y2,…,yk,….
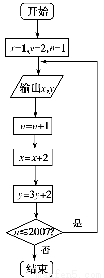
(1)分别求数列{xk}和{yk}的通项公式;
(2)令zk=xkyk,求数列{zk}的前k项和Tk,其中k∈N*,k≤2 007.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第1课时练习卷(解析版) 题型:选择题
若数列{an}是等差数列,则数列{bn} 也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为( )
A.dn=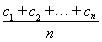 B.dn=
B.dn=
C.dn=  D.dn=
D.dn=
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:填空题
在△ABC中,AB=10,AC=6,O为BC的垂直平分线上一点,则 ·
· =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知向量 =(cos α,sin α),将向量
=(cos α,sin α),将向量 绕坐标原点O逆时针旋转θ角得到向量
绕坐标原点O逆时针旋转θ角得到向量 (0°<θ<90°),则下列说法不正确的为( )
(0°<θ<90°),则下列说法不正确的为( )
A.| +
+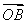 |=|
|=| -
- | B.|
| B.|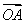 |+|
|+|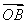 |>|
|>| -
- |
|
C.(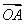 +
+ )⊥(
)⊥(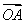 -
- ) D.
) D.  、
、 在
在 +
+ 方向上的投影相等
方向上的投影相等
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:选择题
在△ABC中,∠ABC=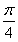 ,AB=
,AB=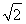 ,BC=3,则sin∠BAC=( )
,BC=3,则sin∠BAC=( )
A. 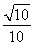 B.
B.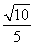 C.
C.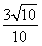 D.
D.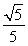
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:选择题
设P和Q是两个集合,定义集合P-Q={x|x∈P,且x∉Q},如果P={x|log2x<1},Q={x||x-2|<1},那么P-Q等于( )
A.{x|0<x<1} B.{x|0<x≤1}
C.{x|1<x<2} D.{x|2<x<3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com