
根据如图所示的程序框图,将输出的x,y值依次分别记为x1,x2,…,xk,…;y1,y2,…,yk,….
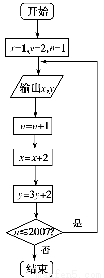
(1)分别求数列{xk}和{yk}的通项公式;
(2)令zk=xkyk,求数列{zk}的前k项和Tk,其中k∈N*,k≤2 007.
(1)yk=3k-1(k∈N*,k≤2 007).(2)(k-1)·3k+1+3+k2
【解析】(1)由框图,知数列{xk}中,x1=1,xk+1=xk+2,
∴xk=1+2(k-1)=2k-1(k∈N*,k≤2 007)
由框图,知数列{yk}中,yk+1=3yk+2,
∴yk+1+1=3(yk+1)∴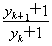 =3,y1+1=3.
=3,y1+1=3.
∴数列{yk+1}是以3为首项,3为公比的等比数列,
∴yk+1=3·3k-1=3k,∴yk=3k-1(k∈N*,k≤2 007).
(2)Tk=x1y1+x2y2+…+xkyk=1×(3-1)+3×(32-1)+…+(2k-1)(3k-1)=1×3+3×32+…+(2k-1)·3k-[1+3+…+(2k-1)]
记Sk=1×3+3×32+…+(2k-1)·3k ①
则3Sk=1×32+3×33+…+(2k-1)·3k+1 ②
①-②,得-2Sk=3+2·32+2·33+…+2·3k-(2k-1)·3k+1
=2(3+32+…+3k)-3-(2k-1)·3k+1=2×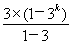 -3-(2k-1)·3k+1
-3-(2k-1)·3k+1
=3k+1-6-(2k-1)·3k+1=2(1-k)·3k+1-6
∴Sk=(k-1)·3k+1+3∴Tk=(k-1)·3k+1+3+k2


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第3课时练习卷(解析版) 题型:解答题
已知椭圆E: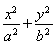 =1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2
=1(a>b>0)的右焦点为F,过原点和x轴不重合的直线与椭圆E相交于A,B两点,且|AF|+|BF|=2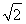 ,|AB|的最小值为2.
,|AB|的最小值为2.
(1)求椭圆E的方程;
(2)若圆x2+y2=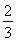 的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
的切线L与椭圆E相交于P,Q两点,当P,Q两点横坐标不相等时,OP(O为坐标原点)与OQ是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:选择题
已知命题“如果x⊥y,y∥z,则x⊥z”是假命题,那么字母x,y,z在空间所表示的几何图形可能是( )
A.全是直线 B.全是平面
C.x,z是直线,y是平面 D.x,y是平面,z是直线
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:解答题
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:选择题
把70个面包分五份给5个人,使每人所得成等差数列,且使较大的三份之和的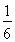 是较小的两份之和,则最小的一份为( )
是较小的两份之和,则最小的一份为( )
A.2 B.8
C.14 D.20
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(解析版) 题型:解答题
已知向量a=(cos α,sin α),b=(cos x,sin x),c=(sin x+2sin α,cos x+2cos α),其中0<α<x<π.
(1)若α= ,求函数f(x)=b·c的最小值及相应x的值;
,求函数f(x)=b·c的最小值及相应x的值;
(2)若a与b的夹角为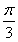 ,且a⊥c,求tan 2α的值.
,且a⊥c,求tan 2α的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
在四边形ABCD中,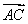 =(1,2),
=(1,2),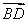 =(-4,2),则该四边形的面积为( )
=(-4,2),则该四边形的面积为( )
A.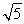 B.2
B.2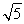 C.5 D.10
C.5 D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
A.存在极大值 B.存在极小值
C.是增函数 D.是减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com