练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
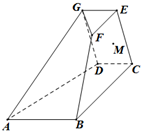
    如图所示几何体中，AB∥CD∥EG，∠ABC=90°，CD=EG=
    1
    2
    AB，平面BCEF⊥平面ABCD，点M为侧面BCEF内的一个动点，若点M到直线EG的距离与到平面ABCD的距离相等，则点M在侧面BCEF内的轨迹是（　　）
    A、一条线段
    B、圆的一部分
    C、抛物线的一部分
    D、椭圆的一部分
    考点：轨迹方程
    专题：综合题,圆锥曲线的定义、性质与方程
    分析：先证明EG⊥平面BCEF，可得ME为点M到直线EG的距离，由点M到直线EG的距离与到平面ABCD的距离相等，可得M到定点E的距离等于M到直线BC的距离，利用抛物线的定义，即可得出结论．
    解答：解：∵∠ABC=90°，平面BCEF⊥平面ABCD，
    ∴AB⊥平面BCEF，
    ∵AB∥EG，
    ∴EG⊥平面BCEF，
    ∵EM?平面BCEF，
    ∴EG⊥EM，即ME为点M到直线EG的距离，
    ∵点M到直线EG的距离与到平面ABCD的距离相等，
    ∴M到定点E的距离等于M到直线BC的距离，
    ∴点M在侧面BCEF内的轨迹是抛物线的一部分．
    故选：C．
    点评：本题考查轨迹方程，考查抛物线的定义，考查线面垂直，考查学生分析解决问题的能力，正确运用抛物线的定义是关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列各组对象中不能形成集合的是（　　）
    A、高一数学课本中较难的题
    B、高二（2）班学生家长全体
    C、高三年级开设的所有课程
    D、高一（12）班个子高于1.7m的学生

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆O：x2+y2=4与x轴的正半轴相交于A点，C，D两点在圆O上，C在第一象限，D在第二象限，C，D的横坐标分别为
    10
    13
    ，-
    8
    5
    ，则cos∠COD=（　　）
    A、-
    16
    65
    B、
    16
    65
    C、-
    56
    65
    D、
    56
    65

    查看答案和解析>>

    科目：高中数学 来源： 题型：

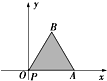    将边长为2的等边△PAB沿x轴正方向滚动，某时刻P与坐标原点重合（如图），设顶点P（x，y）的轨迹方程是y=f（x），关于函数y=f（x）的有下列说法：
    ①f（x）的值域为[0，2]；
    ②f（x）是周期函数；
    ③f（4.1）＜f（π）＜f（2013）；
    ④∫
     
    6
    0
    f（x）dx=
    9π
    2
    ．
    其中正确的说法个数为（　　）
    A、0B、1C、2D、3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知⊙A1：（x+2）2+y2=12和点A2（2，0），则过点A2且与⊙A1相切的动圆圆心P的轨迹方程为（　　）
    A、
    x2
    3
    -y2=1
    B、
    x2
    3
    +y2=1
    C、x2-y2=2
    D、
    x2
    12
    +
    y2
    8
    =1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知方程x2+y2+2x-y+m=0表示圆，则实数m的取值范围是（　　）
    A、m＞
    5
    4
    B、m＞-
    5
    4
    C、m＜
    5
    4
    D、m＜-
    5
    4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    自平面上一点O引两条射线OA，OB，点P在OA上运劝，点Q在OB上运动且保持|
    PQ
    |    为定值a（点P，Q不与点O重合），已知∠AOB=60°，a=
    		7
    ，则
    PQ
    •
    PO
    |
    PO
    |
    +
    3
    QP
    •
    QO
    |
    QO
    |
    的取值范围为（　　）
    A、（
    1
    2
    ，
    		7
    ]
    B、（
    		7
    2
    ，
    		7
    ]
    C、（-
    1
    2
    ，
    		7
    ]
    D、（-
    		7
    2
    ，7]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若0＜α＜
    π
    4
    ，则下列判断正确的是（　　）
    A、cosα＜sinα
    B、cosα＞sinα
    C、cosα=sinα
    D、以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于两个变量y，x进行回归分析时，分别选择了4个模型，它们的相关指数R2如下，其中拟合效果最好的模型是（　　）
    A、模型1，相关指数R2为0.89
    B、模型2，相关指数R2为0.98
    C、模型3，相关指数R2为0.09
    D、模型4，相关指数R2为0.50

    查看答案和解析>>

    同步练习册答案