解:(1)当k=0 时,f(x) 是偶函数;
当k≠0 时,f(x) 既不是奇函数,也不是偶函数.
证明:①当k=0 时,f(x)=x
2 (x≠0 ),
∴f(-x)=(-x)
2=x
2=f(x),
∴f(x) 是偶函数;
②当k≠0 时,f(-1)=1-k,f(1)=1+k,
∴f(-1)+f(1)=1-k+1+k=2≠0,
∴f(-1)≠-f(1);
又f(-1)-f(1)=1-k-1-k=-2k≠0,
∴f(-1)≠f(1).
∴f(x)
既不是奇函数,也不是偶函数.
(2)由f(x)=f(a) 得,

,
化简整理得,

,
由x-a=0 得,方程的一个解x
1=a;
由

得,ax
2+a
2x-8=0,①
∵a>3
,∴△=a
4+32a>0,
解①得

,

,
∵x
2<0,x
3>0,∴x
2<x
3,
又x
1>0,∴x
1>x
2.
若x
1=x
3,即

,
则

,
∴a
4=4a,解得a=0 或

,与a>3 矛盾,∴x
1≠x
3 故原方程有三个实数解.
分析:(1)由已知易判断出函数的定义域为R,关于原点对称,再判断f(-x)与f(x)的关系,即可根据函数奇偶性的定义,进行判断得到结论;
(2)先由f(x)=f(a) 得,

,化简整理得,

由x-a=0 得,方程的一个解x
1=a;由

得,ax
2+a
2x-8=0,①解①得 有两个解,从而得出故原方程有三个实数解.
点评:本小题主要考查根的存在性及根的个数判断、函数奇偶性的应用等基础知识,考查运算求解能力与转化思想.属于基础题.

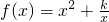 (x≠0,常数k∈R).
(x≠0,常数k∈R). ,
, ,
, 得,ax2+a2x-8=0,①
得,ax2+a2x-8=0,① ,
, ,
, ,
, ,
, ,与a>3 矛盾,∴x1≠x3
,与a>3 矛盾,∴x1≠x3  ,化简整理得,
,化简整理得, 由x-a=0 得,方程的一个解x1=a;由
由x-a=0 得,方程的一个解x1=a;由 得,ax2+a2x-8=0,①解①得 有两个解,从而得出故原方程有三个实数解.
得,ax2+a2x-8=0,①解①得 有两个解,从而得出故原方程有三个实数解.
