
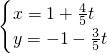 (t为参数)与曲线C的极坐标方程:
(t为参数)与曲线C的极坐标方程: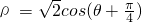 .
.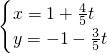 消去t得直线l普通方程3x+4y+1=0…(2分).
消去t得直线l普通方程3x+4y+1=0…(2分).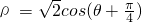 化为
化为 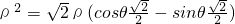 …(4分),
…(4分),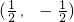 ,半径为
,半径为 ,…(8分)
,…(8分)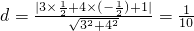 ,…(10分)
,…(10分)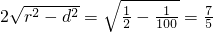 . …(12分)
. …(12分)

科目:高中数学 来源:2012年江西省抚州市临川一中高三4月模拟数学试卷(理科)(解析版) 题型:解答题
 ,对任意的x∈R恒成立,则实数a的取值范围是______
,对任意的x∈R恒成立,则实数a的取值范围是______ (t为参数),圆C:ρ=2
(t为参数),圆C:ρ=2 cos(θ-
cos(θ- )(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______
)(极轴与x轴的非负半轴重合,且单位长度相同),若直线l被圆C截得弦长为2,则a=______查看答案和解析>>
科目:高中数学 来源:2013年福建省泉州市惠安三中高考数学模拟试卷(理科)(解析版) 题型:解答题
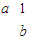 )有特征值λ1=2及对应的一个特征向量
)有特征值λ1=2及对应的一个特征向量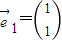 .
.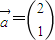 ,求
,求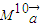 .
.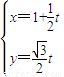 (t为参数),曲线C1:
(t为参数),曲线C1: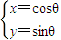 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的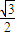 倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2C,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.查看答案和解析>>
科目:高中数学 来源:2012年辽宁省大连市高考数学压轴卷 (理科)(解析版) 题型:解答题
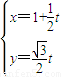 (t为参数),曲线C1:
(t为参数),曲线C1: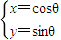 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省洛阳市示范高中高三联考数学试卷(理科)(解析版) 题型:解答题
 (t为参数),曲线C1:
(t为参数),曲线C1: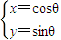 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的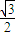 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.查看答案和解析>>
科目:高中数学 来源:2012年辽宁省大连市高考数学压轴卷 (文科)(解析版) 题型:解答题
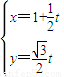 (t为参数),曲线C1:
(t为参数),曲线C1: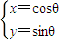 (θ为参数).
(θ为参数). 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的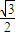 倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
倍,得到曲线C2,设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com