Question

【题目】已知曲线是中心在原点，焦点在轴上的双曲线的右支，它的离心率刚好是其对应双曲线的实轴长，且一条渐近线方程是，线段是过曲线右焦点的一条弦，是弦的中点。

（1）求曲线的方程；

（2）求点到轴距离的最小值；

（3）若作出直线，使点在直线上的射影满足.当点在曲线上运动时，求的取值范围.

（参考公式：若为双曲线右支上的点，为右焦点，则.（为离心率））

Answer 1

【答案】（1）； （2）点到轴距离的最小值为；（3）.

【解析】

（1）根据已知设双曲线的右支方程，离心率刚好是其对应双曲线的实轴长，可以得到的关系，一条渐近线方程是，可以得到的关系，而，三个等式联立，可以求出的值，最后求出双曲线的右支方程，别忘记写上的取值范围。

（2）根据斜率是否存在进行分类讨论：当存在斜率时，设出直线方程与双曲线右支方程联立，求出满足条件的斜率取值范围，根据一元二次方程根与系数的关系求出点的横坐标的大小，求出点到轴距离的取值范围。当不存在斜率时，求出点到轴距离，综合两种情形得出结论。

（3）由可以得到，这样可以求出与的关系，由焦半径公式可以求出，两个式子联立，可以求出点的横坐标，利用（2）的结论，可以求出的取值范围。

（1）设，离心率刚好是其对应双曲线的实轴长，所以有①，一条渐近线方程是所以有②，而③，三个方程联立，可求出，所以曲线的方程是：

（2）由（1）知，曲线的右焦点的坐标为，若弦的斜率存在，

则弦的方程为：，代入双曲线方程得：

.

设点， ，

由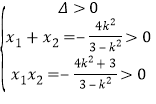，解得：，点到轴距离：

而当弦的斜率不存在时，点到轴距离。

所以点到轴距离的最小值为.

（3）点在直线上的射影满足，

，到直线的距离……①

由焦半径公式

……②

将②代入①，得：

，， .