
分析 由f(x)=0得$\frac{[x]}{x}$=a,令g(x)=$\frac{[x]}{x}$,作出g(x)的图象,利用数形结合即可得到a的取值范围.
解答 解:由f(x)=$\frac{[x]}{x}$-a=0得$\frac{[x]}{x}$=a,
设g(x)=$\frac{[x]}{x}$,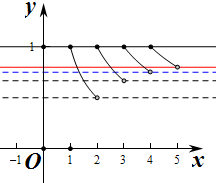
则当0<x<1,[x]=0,此时g(x)=0,
当1≤x<2,[x]=1,此时g(x)=$\frac{1}{x}$,此时$\frac{1}{2}$<g(x)≤1,
当2≤x<3,[x]=2,此时g(x)=$\frac{2}{x}$,此时$\frac{2}{3}$<g(x)≤1,
当3≤x<4,[x]=3,此时g(x)=$\frac{3}{x}$,此时$\frac{3}{4}$<g(x)≤1,
当4≤x<5,[x]=4,此时g(x)=$\frac{4}{x}$,此时$\frac{4}{5}$<g(x)≤1,
作出函数g(x)的图象,
要使f(x)=$\frac{[x]}{x}$-a有且仅有两个零点,
即函数g(x)=a有且仅有两个零点,
则由图象可知$\frac{2}{3}$<a≤$\frac{3}{4}$,
故答案为:($\frac{2}{3}$,$\frac{3}{4}$].
点评 本题主要考查函数零点的应用,根据函数和方程之间的关系构造函数g(x),利用数形结合是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
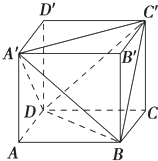 如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | $-\frac{{2\sqrt{2}}}{5}$ | C. | $\frac{{4\sqrt{2}}}{5}$ | D. | $-\frac{{4\sqrt{2}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
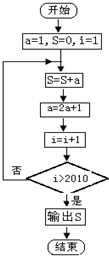 如图是计算首项为1的数列{an}前m项和Sn的算法框图,
如图是计算首项为1的数列{an}前m项和Sn的算法框图,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com