
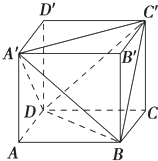
 如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:分析 (1)利用割补法,求三棱锥A′-BC′D的体积.
(2)分别求出球O1,O2,O3半径,即可求球O1,O2,O3半径的比值.
解答 解:(1)三棱锥A′-BC′D的体积=a3-4×$\frac{1}{3}×\frac{1}{2}×a×a×a$=$\frac{1}{3}{a}^{3}$;
(2)设三棱锥A′-BC′D的六条棱长为1个单位,则棱锥的高为$\frac{\sqrt{6}}{3}$,O2,O3半径为$\frac{\sqrt{6}}{4}$,$\frac{\sqrt{6}}{12}$,O2与O3半径比为3:1,
三棱锥对棱的距离为$\sqrt{\frac{3}{4}-\frac{1}{4}}$=$\frac{\sqrt{2}}{2}$,所以球O1半径为$\frac{\sqrt{2}}{4}$,
∴球O1,O2,O3半径的比值为$\sqrt{3}$:3:1.
点评 本题考查体积的计算,考查学生的计算能力,正确计算是关键.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin1.5<sin3<cos8.5 | B. | cos8.5<sin3<sin1.5 | ||
| C. | sin1.5<cos8.5<sin3 | D. | cos8.5<sin1.5<sin3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (0,1)∪(1,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2016 | C. | -2015 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com