
分析 (1)利用导数的几何意义即可求解;
(2)先求函数导数,再讨论参数范围确定导数符号即可.
(3)由条件得到不等关系,再进行整体换元转化为一元不等式的证明问题.
解答 解:(1)当a=1时,g(x)=lnx+x2-3x,x>0,
∴$g′(x)=\frac{1}{x}+2x-3$,
∴g′(1)=0,又g(1)=-2,
∴曲线在x=1处的切线方程为y=-2.
(2)∵$g′(x)=\frac{1}{x}+2ax-(2a+1)$
=$\frac{2a{x}^{2}-(2a+1)x+1}{x}$
=$\frac{(2ax-1)(x-1)}{x}$=$\frac{2a(x-\frac{1}{2a})(x-1)}{x}$(x>0)
∴①当$\frac{1}{2a}<1$,即$a>\frac{1}{2}$时,令g'(x)>0得,$0<x<\frac{1}{2a}$或x>1;
令g'(x)<0得,$\frac{1}{2a}<x<1$.
所以,增区间为$(0\;,\;\frac{1}{2a})\;,\;(1,+∞)$;减区间为$(\frac{1}{2a}\;,\;1)$;
②当$\frac{1}{2a}>1$,即$0<a<\frac{1}{2}$时,令g'(x)>0得,0<x<1或$x>\frac{1}{2a}$;
令g'(x)<0得,$\frac{1}{2a}<x<1$.
所以,增区间为$(0\;,\;1)\;,\;(\frac{1}{2a},+∞)$;减区间为$(\frac{1}{2a}\;,\;1)$;
③当$\frac{1}{2a}=1$,即$a=\frac{1}{2}$时,$g'(x)=\frac{{{{(x-1)}^2}}}{x}>0$,增区间为(0,+∞).
综上,当$0<a<\frac{1}{2}$时,增区间为$(0\;,\;1)\;,\;(\frac{1}{2a},+∞)$;减区间为$(1\;,\;\frac{1}{2a})$;
当$a=\frac{1}{2}$时,增区间为(0,+∞);
当$a>\frac{1}{2}$时,增区间为$(0\;,\;\frac{1}{2a})\;,\;(1,+∞)$;减区间为$(\frac{1}{2a}\;,\;1)$.
(3)依题,$k=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{ln{x_2}-ln{x_1}}}{{{x_2}-{x_1}}}$,要证 $\frac{1}{x_2}<k<\frac{1}{x_1}$,
只要证 $\frac{1}{{x}_{2}}<\frac{ln{x}_{2}-ln{x}_{1}}{{x}_{2}-{x}_{1}}<\frac{1}{{x}_{1}}$,
因为 x2-x1>0,故只要证 $\frac{{x}_{2}-{x}_{1}}{{x}_{2}}<ln\frac{{x}_{2}}{{x}_{1}}<\frac{{x}_{2}-{x}_{1}}{{x}_{1}}$,
令$\frac{{x}_{2}}{{x}_{1}}=t$(t>1),则只需证 $1-\frac{1}{t}<lnt<t-1$(t>1),
令$h(t)=lnt+\frac{1}{t}-1$(t>1),则$h′(t)=\frac{1}{t}-\frac{1}{{t}^{2}}=\frac{t-1}{{t}^{2}}$>0,
∴h(t)在(1,+∞)上单调递增,
∴h(t)>h(1)=0,即$lnt>1-\frac{1}{t}$(t>1),
同理可证:lnt<t-1,
综上,$1-\frac{1}{t}<lnt<t-1$(t>1),即$\frac{1}{{x}_{2}}<k<\frac{1}{{x}_{1}}$.
点评 本题考查了导数的几何意义和导数在函数中的运用.考查了逻辑思维和运算能力以及转化的思想方法.属于难题.


科目:高中数学 来源: 题型:解答题
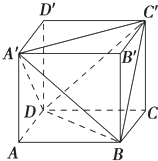 如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3 ) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
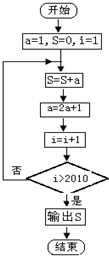 如图是计算首项为1的数列{an}前m项和Sn的算法框图,
如图是计算首项为1的数列{an}前m项和Sn的算法框图,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>2,x<-3 | B. | {x|x>2,x<-3} | C. | (-∞,-2)∪(3,+∞) | D. | x>3,x<-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com