
【题目】我国南宋数学家杨辉在所著的《详解九章算法》一书中用如图所示的三角形解释二项展开式的系数规律,去掉所有为1的项,依次构成2,3,3,4,6,4,5,10,10,5,6…,则此数列的前50项和为( )

A.2025B.3052C.3053D.3049
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,则( )
,则( )
A.双曲线C的离心率等于半焦距的长
B.双曲线![]() 与双曲线C有相同的渐近线
与双曲线C有相同的渐近线
C.双曲线C的一条准线被圆x2+y2=1截得的弦长为![]()
D.直线y=kx+b(k,b![]() R)与双曲线C的公共点个数只可能为0,1,2
R)与双曲线C的公共点个数只可能为0,1,2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在以![]() 为圆心,6为半径的圆
为圆心,6为半径的圆![]() 内有一点
内有一点![]() ,点
,点![]() 为圆
为圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 交于点
交于点![]() .
.
(1)判断点![]() 的轨迹是什么曲线,并求其方程;
的轨迹是什么曲线,并求其方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值;
的最大值;
(3)在圆![]() 上的任取一点
上的任取一点![]() ,作曲线
,作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 、
、![]() ,试判断
,试判断![]() 与
与![]() 是否垂直,并给出证明过程.
是否垂直,并给出证明过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车在行驶中,由于惯性,刹车后还要继续向前滑行一段距离才能停止,一般称这段距离为“刹车距离”.刹车距离是分析交通事故的一个重要依据.在一个限速为![]() 的弯道上,甲、乙两辆汽车相向而行,突然发现有危险情况,同时紧急刹车,但还是发生了交通事故.事后现场勘查,测得甲车的刹车距离略超过
的弯道上,甲、乙两辆汽车相向而行,突然发现有危险情况,同时紧急刹车,但还是发生了交通事故.事后现场勘查,测得甲车的刹车距离略超过![]() ,乙车的刹车距离略超过
,乙车的刹车距离略超过![]() .已知甲、乙两种车型的刹车距离
.已知甲、乙两种车型的刹车距离![]() 与车速
与车速![]() 之间的关系分别为:
之间的关系分别为:![]() ,
,![]() .根据以上信息判断:在这起交通事故中,应负主要责任的可能是_______________车,理由是__________________________.
.根据以上信息判断:在这起交通事故中,应负主要责任的可能是_______________车,理由是__________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领广大农村地区人民群众脱贫奔小康。经过不懈的奋力拼搏,新农村建设取得巨大进步,农民年收入也逐年增加。为了更好的制定2019年关于加快提升农民年收人力争早日脱贫的工作计划,该地扶贫办统计了2018年50位农民的年收人并制成如下频率分布直方图:

(1)根据频率分布直方图,估计50位农民的年平均收入![]() (单位:千元)(同一组数据用该组数据区间的中点值表示);
(单位:千元)(同一组数据用该组数据区间的中点值表示);
(2)由频率分布直方图,可以认为该贫困地区农民年收入![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为年平均收入
近似为年平均收入![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求:
.利用该正态分布,求:
(i)在2019年脱贫攻坚工作中,若使该地区约有占总农民人数的![]() 的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
的农民的年收入高于扶贫办制定的最低年收入标准,则最低年收入大约为多少千元?
(ii)为了调研“精准扶贫,不落一人”的政策要求落实情况, 扶贫办随机走访了1000位农民。若每个农民的年收人相互独立,问:这1000位农民中的年收入不少于12.14千元的人数最有可能是多少?
附:参考数据与公式![]() ,若
,若![]() ~
~![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只昆虫的产卵数![]() 与温度
与温度![]() 有关,现收集了6组观测数据与下表中.由散点图可以发现样本点分布在某一指数函数曲线
有关,现收集了6组观测数据与下表中.由散点图可以发现样本点分布在某一指数函数曲线![]() 的周围.
的周围.
温度 | 21 | 23 | 25 | 27 | 29 | 31 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 114 |
令![]() ,经计算有:
,经计算有:
|
|
|
|
|
|
26 | 40.5 | 19.50 | 6928 | 526.60 | 70 |
(1)试建立![]() 关于
关于![]() 的回归直线方程并写出
的回归直线方程并写出![]() 关于
关于![]() 的回归方程
的回归方程![]() .
.
(2)若通过人工培育且培育成本![]() 与温度
与温度![]() 和产卵数
和产卵数![]() 的关系为
的关系为![]() (单位:万元),则当温度为多少时,培育成本最小?
(单位:万元),则当温度为多少时,培育成本最小?
注:对于一组具有线性相关关系的数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘公式分别为
的斜率和截距的最小二乘公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知![]() 是直线
是直线![]() 上的动点,点
上的动点,点![]() 的坐标是
的坐标是![]() ,过
,过![]() 的直线
的直线![]() 与
与![]() 垂直,并且
垂直,并且![]() 与线段
与线段![]() 的垂直平分线相交于点
的垂直平分线相交于点![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设曲线![]() 上的动点
上的动点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的另一个交点为
的另一个交点为![]() (
(![]() 与
与![]() 不重合),是否存在一个定点
不重合),是否存在一个定点![]() ,使得
,使得![]() 三点共线?若存在,求出点
三点共线?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,点
,点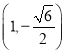 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)圆![]() 是以椭圆
是以椭圆![]() 的焦距为直径的圆,点
的焦距为直径的圆,点![]() 是椭圆
是椭圆![]() 的右顶点,过点
的右顶点,过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,若
,若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com