
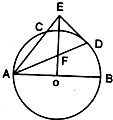
 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.求证:ED是⊙O的切线.科目:高中数学 来源: 题型:
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 销售量y(百件) | 4 | 4 | 5 | 6 | 6 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| ? |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 测试指标分组 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] | |
| 频 数 |
装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 | |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为
从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中的视力情况进行统计,其频率分布直方图如图所示.若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为查看答案和解析>>
科目:高中数学 来源: 题型:
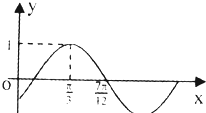 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| π |
| 6 |
A、{x|x=kπ-
| ||
B、{x|x=kπ-
| ||
C、{x|x=2kπ-
| ||
D、{x|x=2kπ-
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com