
分析 通过函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的定义域为R可得△=a2-4<0,通过函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的值域为R可得△=a2-4≥0,进而可得结论.
解答 解:若函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的定义域为R,
则有:x2-ax+1>0的解集为R,
∴△=a2-4<0,
∴-2<a<2;
若函数$f(x)={log_{\frac{1}{2}}}({{x^2}-ax+1})$的值域为R,
则有:x2-ax+1>0恒成立,
∴△=a2-4≥0,
∴a≤-2或a≥2;
故答案分别为:(-2,2),(-∞,-2]∪[2,+∞).
点评 本题考查对数函数的简单性质,注意解题方法的积累,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
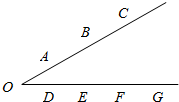 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 内切 | C. | 内含 | D. | 外切 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{16}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| B. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{6}$个单位长度,再把横坐标缩短为原来的2倍(纵坐标不变) | |
| D. | 向左平移$\frac{π}{3}$个单位长度,再把横坐标缩短为原来的$\frac{1}{2}$倍(纵坐标不变) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-2 | B. | 9x+y+16=0 | C. | 9x+y-16=0 | D. | 9x+y-16=0或y=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com