
分析 (I)点M、N的极坐标分别为(3,π),($\sqrt{3}$,$\frac{π}{2}$),利用极坐标与直角坐标互化公式可得直角坐标,进而得到直线l的方程.当OP⊥MN时,线段OP取得最小值,此时直线OP的斜率为-$\sqrt{3}$.可得直线OP的方程,联立即可解得P坐标.
(II)线段MN的中点C$(-\frac{3}{2},\frac{\sqrt{3}}{2})$,可得以MN为直径的圆C的标准方程为:$(x+\frac{3}{2})^{2}+(y-\frac{\sqrt{3}}{2})^{2}$=3.利用cos2θ+sin2θ=1可以化为参数方程.利用点到直线的距离公式可得圆心C到直线l的距离d,在(Ⅰ)的条件下直线OP与圆C相交所得的弦长=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:(I)点M、N的极坐标分别为(3,π),($\sqrt{3}$,$\frac{π}{2}$),可得直角坐标分别为:(-3,0),$(0,\sqrt{3})$.
可得直线l的方程:$y=\frac{\sqrt{3}}{3}$x+$\sqrt{3}$.
当OP⊥MN时,线段OP取得最小值,此时直线OP的斜率为-$\sqrt{3}$.
∴直线OP的方程为:y=-$\sqrt{3}$x.联立$\left\{\begin{array}{l}{y=-\sqrt{3}x}\\{y=\frac{\sqrt{3}}{3}x+\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{3}{4}}\\{y=\frac{3\sqrt{3}}{4}}\end{array}\right.$.
∴P$(-\frac{3}{4},\frac{3\sqrt{3}}{4})$.
(II)线段MN的中点C$(-\frac{3}{2},\frac{\sqrt{3}}{2})$,∴以MN为直径的圆C的标准方程为:$(x+\frac{3}{2})^{2}+(y-\frac{\sqrt{3}}{2})^{2}$=3.
化为参数方程:$\left\{\begin{array}{l}{x=-\frac{3}{2}+\sqrt{3}cosθ}\\{y=\frac{\sqrt{3}}{2}+\sqrt{3}sinθ}\end{array}\right.$(θ为参数).
∵圆心C到直线l的距离d=$\frac{|-\frac{3\sqrt{3}}{2}+\frac{\sqrt{3}}{2}|}{2}$=$\frac{\sqrt{3}}{2}$,
∴在(Ⅰ)的条件下直线OP与圆C相交所得的弦长=2$\sqrt{3-(\frac{\sqrt{3}}{2})^{2}}$=3.
点评 本题考查了极坐标与直角坐标方程的互化、参数方程化为普通方程、点到直线的距离公式、直线与圆相交弦长公式,考查了推理能力与计算能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
 如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )
如图,以△ABC的BC边为直径的半圆交AB于点D,交AC于点E,EF⊥BC于F,BF:FC=5:1,AB=8,AE=2,则AD长为( )| A. | $\frac{{1+\sqrt{21}}}{2}$ | B. | $\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | $\frac{43}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
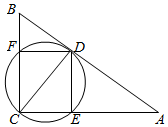 如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.
如图,在三角形ABC中,∠ACB=90°,CD⊥AB于D,以CD为直径的圆分别交AC、BC于E、F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或0<x<1} | D. | {x|x<-1或x>1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com